Giải VTH Toán 9 KNTT Bài tập ôn tập cuối năm có đáp án

a) Với x ≥ 0, ta có:

\(P = \frac{{x\sqrt x - x + 2\sqrt x + 4}}{{x\sqrt x + 8}}\)

\( = \frac{{x\sqrt x + 8 - \left( {x - 2\sqrt x + 4} \right)}}{{\sqrt x + 8}}\)

\( = 1 - \frac{{x - 2\sqrt x + 4}}{{\sqrt x + 8}}\)

\( = 1 - \frac{{x - 2\sqrt x + 4}}{{\left( {\sqrt x + 2} \right)\left( {x - 2\sqrt x + 4} \right)}}\)

\( = 1 - \frac{1}{{\sqrt x + 2}}.\)

Vậy với x ≥ 0 thì \(P = 1 - \frac{1}{{\sqrt x + 2}}.\)

b) Thay x = 64 (thỏa mãn x ≥ 0) vào biểu thức \(P = 1 - \frac{1}{{\sqrt x + 2}},\) ta được:

\(P = 1 - \frac{1}{{\sqrt {64} + 2}} = 1 - \frac{1}{{8 + 2}} = 1 - \frac{1}{{10}} = \frac{9}{{10}}.\)

Vậy giá trị của biểu thức P bằng \(\frac{9}{{10}}\) khi x = 64.

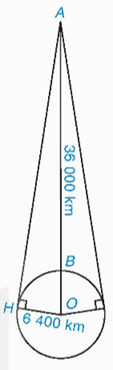
Áp dụng định lí Pythagore cho tam giác AHO vuông tại H, ta có:

AO² = AH² + HO²

Suy ra AH² = AO² – HO² = (AB + BO)² – HO²

                   = (36 000 + 6 400)² – 6 400²

                   = 42 400² – 6 400² = 1 756 800 000.

Do đó AH ≈ 41 914 (km).

Vậy vị trí xa nhất trên bề mặt Trái Đất có thể nhận được tín hiệu từ vệ tinh cách vệ tinh khoảng 41 914 kilômét.

a) –6x + 3(x + 1) > 4x – (x – 4)

–6x + 3x + 3 > 4x – x + 4

–3x + 3 > 3x + 4

–3x – 3x > 4 – 3

–6x > 1

    \(x < - \frac{1}{6}.\)

Vậy bất phương trình có nghiệm là \(x < - \frac{1}{6}.\)

b) (2x + 1)(2x – 1) < 4x² – 4x + 1

4x² – 1 < 4x² – 4x + 1

4x² – 4x² + 4x  < 1 + 1

4x < 2

\(x < \frac{1}{2}.\)

Vậy bất phương trình có nghiệm là \(x < \frac{1}{2}.\)

a) Điều kiện xác định: x ≠ –1.

\(\frac{2}{{x + 1}} - \frac{{2x}}{{{x^2} - x + 1}} = \frac{3}{{{x^3} + 1}}\)

\(\frac{{2\left( {{x^2} - x + 1} \right)}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} - \frac{{2x \cdot \left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} = \frac{3}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}}\)

2(x² – x + 1) – 2x(x + 1) = 3

2x² – 2x + 2 – 2x² – 2x = 3

–4x + 2 = 3

–4x = 1

\(x = - \frac{1}{4}\) (thỏa mãn điều kiện).

Vậy phương trình đã cho có nghiệm là \(x = - \frac{1}{4}.\)

b) Điều kiện xác định: \(x \ne \frac{1}{2}\) và \(x \ne - \frac{1}{2}.\)

\(\frac{{x + 1}}{{2x - 1}} - \frac{2}{{2x + 1}} = \frac{{2{x^2}}}{{4{x^2} - 1}}\)

\(\frac{{\left( {x + 1} \right)\left( {2x + 1} \right)}}{{\left( {2x - 1} \right)\left( {2x + 1} \right)}} - \frac{{2\left( {2x - 1} \right)}}{{\left( {2x - 1} \right)\left( {2x + 1} \right)}} = \frac{{2{x^2}}}{{\left( {2x - 1} \right)\left( {2x + 1} \right)}}\)

(x + 1)(2x + 1) – 2(2x – 1) = 2x²

2x² + x + 2x + 1 – 4x + 2 = 2x²

2x² – 2x² + x + 2x – 4x = –1 – 2

–x = –3

x = 3 (thỏa mãn điều kiện).

Vậy phương trình đã cho có nghiệm là x = 3.

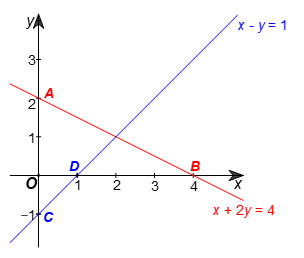
a) ⦁ Vẽ đường thẳng (d₁): x + 2y = 4.

Cho x = 0 thì y = 2, ta được giao điểm của đường thẳng (d₁) với trục tung là A(0; 2).

Cho y = 0 thì x = 4, ta được giao điểm của đường thẳng (d₁) với trục hoành là B(4; 0).

Đường thẳng (d₁) là đường thẳng AB (hình vẽ).

⦁ Vẽ đường thẳng (d₂): x – y = 1.

Cho x = 0 thì y = –1, ta được giao điểm của đường thẳng (d₂) với trục tung là C(0; –1).

Cho y = 0 thì x = 1, ta được giao điểm của đường thẳng (d₂) với trục hoành là D(1; 0).

Đường thẳng (d₂) là đường thẳng CD (hình vẽ).

b) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 4\,\,\,\,\left( 1 \right)}\\{x - y = 1\,\,\,\,\,\,\,\,\,\left( 2 \right)}\end{array}} \right.\)

Trừ từng vế của hai phương trình (1) và (2), ta được:

(x + 2y) – (x – y) = 4 – 1 hay 3y = 3, suy ra y = 1.

Thế y = 1 vào phương trình (2), ta được:

x – 1 = 1 hay x = 2.

Do đó hệ phương trình trên có nghiệm là (2; 1).

Vậy toạ độ giao điểm của hai đường thẳng (d₁) và (d₂) là điểm (2; 1).

a) Với \(m = \sqrt 2 ,\) ta có hệ phương trình: \(\left( I \right)\,\,\,\left\{ {\begin{array}{*{20}{l}}{x\sqrt 2 - 3y = \sqrt 2 \,\,\,\,\left( 1 \right)}\\{2x - 3y\sqrt 2 = 2}\end{array}} \right.\)

Nhân hai vế của phương trình (1) với \(\sqrt 2 ,\) ta được hệ phương trình sau:

\[\left\{ {\begin{array}{*{20}{l}}{2x - 3y\sqrt 2 = 2}\\{2x - 3y\sqrt 2 = 2.}\end{array}} \right.\]

Trừ từng vế hai phương trình của hệ mới, ta được:

0x + 0y = 0. Hệ thức này luôn thỏa mãn với các giá trị tùy ý của x và y.

Với giá trị tùy ý của x, giá trị của y được tính nhờ hệ thức \(x\sqrt 2 - 3y = \sqrt 2 ,\) suy ra \(y = \frac{{\sqrt 2 }}{3}x - \frac{{\sqrt 2 }}{3}.\)

Vậy hệ phương trình (I) có nghiệm là \(\left( {x;\frac{{\sqrt 2 }}{3}x - \frac{{\sqrt 2 }}{3}} \right)\) với x ∈ ℝ.

b) Với \(m = - \sqrt 2 ,\) ta có hệ phương trình: \(\left( {II} \right)\,\,\,\left\{ {\begin{array}{*{20}{l}}{x\sqrt 2 - 3y = - \sqrt 2 \,\,\,\,\left( 2 \right)}\\{2x - 3y\sqrt 2 = 2}\end{array}} \right.\)

Nhân hai vế của phương trình (2) với \(\sqrt 2 ,\) ta được hệ phương trình sau:

\[\left\{ {\begin{array}{*{20}{l}}{2x - 3y\sqrt 2 = - 2}\\{2x - 3y\sqrt 2 = 2.}\end{array}} \right.\]

Trừ từng vế hai phương trình của hệ mới, ta được:

0x + 0y = –4. Phương trình này vô nghiệm.

Vậy hệ phương trình (II) vô nghiệm.

c) Với \(m = 2\sqrt 2 ,\) ta có hệ phương trình: \(\left( {III} \right)\,\,\,\left\{ {\begin{array}{*{20}{l}}{x\sqrt 2 - 3y = 2\sqrt 2 \,\,\,\,\left( 3 \right)}\\{8x - 3y\sqrt 2 = 2}\end{array}} \right.\)

Nhân hai vế của phương trình (3) với \(\sqrt 2 ,\) ta được hệ phương trình sau:

\(\left\{ {\begin{array}{*{20}{l}}{2x - 3y\sqrt 2 = 4}\\{8x - 3y\sqrt 2 = 2}\end{array}} \right.\)

Trừ từng vế hai phương trình của hệ mới, ta được:

–6x = 2, suy ra \(x = - \frac{1}{3}.\)

Thế \(x = - \frac{1}{3}\) vào phương trình (3), ta được:

\( - \frac{1}{3} \cdot \sqrt 2 - 3y = 2\sqrt 2 ,\) suy ra \(3y = - \frac{{\sqrt 2 }}{3} - 2\sqrt 2 ,\) nên

\(y = - \frac{{\sqrt 2 }}{9} - \frac{{2\sqrt 2 }}{3} = \frac{{ - \sqrt 2 - 2\sqrt 2 \cdot 3}}{9} = \frac{{ - 7\sqrt 2 }}{9}.\)

Vậy hệ phương trình (III) có nghiệm là \(\left( { - \frac{1}{3};\frac{{ - 7\sqrt 2 }}{9}} \right).\)