Giải SGK Toán 9 KNTT Bài 21. Giải bài toán bằng cách lập phương trình có đáp án
81 người thi tuần này 4.6 1.1 K lượt thi 11 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
Gọi x là lãi suất gửi tiết kiệm của bác Lan (x được cho dưới dạng số thập phân) (x > 0).
Số tiền thu được (cả vốn lẫn lãi) của bác Lan sau kì gửi thứ nhất là:
100(1 + x) (triệu đồng).
Số tiền thu được (cả vốn lẫn lãi) của bác Lan sau kì gửi thứ nhất là:
100(1 + x)(1 + x) = 100(1 + x)2 (triệu đồng).
Theo bài, sau hai năm bác Lan rút tiền ra thì nhận được 118,81 triệu đồng cả vốn lẫn lãi nên ta có phương trình:
100(1 + x)2 = 118,81
(1 + x)2 = 1,1881
1 + x = 1,09 (do x > 0).
x = 0,09.
Vậy lãi suất gửi tiết kiệm là 9%.
Lời giải
Số tiền thu được (cả vốn lẫn lãi) của bác Lan sau kì gửi thứ nhất là:
100(1 + x) (triệu đồng).
Lời giải
Số tiền thu được (cả vốn lẫn lãi) của bác Lan sau kì gửi thứ nhất là:
100(1 + x)(1 + x) = 100(1 + x)2 (triệu đồng).
Lời giải
Theo bài, sau hai năm bác Lan rút tiền ra thì nhận được 118,81 triệu đồng cả vốn lẫn lãi nên ta có phương trình:
100(1 + x)2 = 118,81
(1 + x)2 = 1,1881
1 + x = 1,09 (do x > 0).
x = 0,09.
Vậy lãi suất gửi tiết kiệm là 9%.
Lời giải
Gọi x (chiếc) là số xe tải của đội xe (x ∈ ℕ, x > 2).
Số tấn hàng mỗi xe cần chở là: ![]() (tấn).
(tấn).
Số xe tải còn lại sau khi điều chuyển hai xe đi nơi khác là: x – 2 (chiếc).
Lúc này, số tấn hàng mỗi xe phải chở là: ![]() (tấn).
(tấn).
Theo bài, khi làm việc có hai xe phải điều chuyển đi nơi khác nên mỗi xe phải chở thêm 3 tấn hàng nên ta có phương trình:
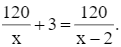
Quy đồng mẫu hai vế của phương trình, ta được:
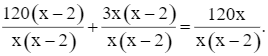
Nhân cả hai vế của phương trình với x(x – 2) để khử mẫu, ta được phương trình:
120(x – 2) + 3x(x – 2) = 120x
120x – 240 + 3x2 – 6x – 120x = 0
3x2 – 6x – 240 = 0
x2 – 2x – 80 = 0
Ta có ∆’ = (–1)2 – 1.(–80) = 81 > 0 và ![]()
Suy ra phương trình trên có hai nghiệm phân biệt:
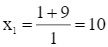 (thỏa mãn điều kiện);
(thỏa mãn điều kiện); 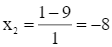 (loại).
(loại).
Vậy đội xe đó có 10 chiếc xe tải.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.