Giải VTH Toán 9 KNTT Luyện tập chung trang 106 có đáp án
37 người thi tuần này 4.6 593 lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề KSCL Toán 9 tháng 10 năm 2026-2027 Trường THCS Từ Liêm 1 (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 10 năm 2026-2027 Trường THCS Kim Giang (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 9 năm 2026-2027 Xã Đại Thanh (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Hồng Vân (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Ngô Sĩ Liên (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Yên Hòa (Hà Nội) có đáp án
Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Giảng Võ (Hà Nội) có đáp án
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
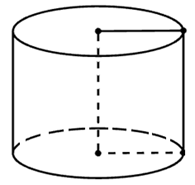
a) V = πR2h mà 2R = h nên \(R = \frac{h}{2},\) suy ra \(V = \pi {\left( {\frac{h}{2}} \right)^2}.h = \pi \frac{{{h^3}}}{4}.\)
Chiều cao của hình trụ là:
\(h = \sqrt[3]{{\frac{{4V}}{\pi }}} = \sqrt[3]{{\frac{{4.2\pi }}{\pi }}} = \sqrt[3]{8} = 2\) (cm).
b) Diện tích xung quanh của hình trụ là:
Sxq = 2πRh = 2π.1.2 = 4π (cm2).
Diện tích hai đáy của hình trụ là:
(cm2).
Diện tích toàn phần của hình trụ là:
Stp = Sxq + Sđáy = 4π + 2π = 6π (cm2).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
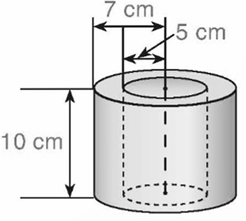
Hình trụ 1 có: R1 = 5 cm; h1 = 10 cm.
Hình trụ 2 có: R2 = 7 cm; h2 = 10 cm.
Thể tích của vòng bi đó là:
V = V2 – V1 = πR22h2 – πR12h1
= π.72.10 – π.52 – 10 = 10π.(72 – 52)
= 10π.24 = 240π (cm3).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
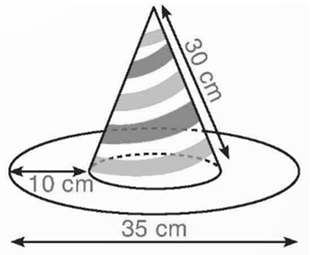
Bán kính đường tròn đáy của hình nón là
(35 – 10.2) : 2 = 7,5 (cm).
Diện tích xung quanh của hình nón là:
S1 = πRl = π.7,5.30 = 225π (cm2).
Diện tích phần vành mũ (hình vành khăn) là:
\({S_2} = \pi .{\left( {17,5} \right)^2} - \pi .{\left( {7,5} \right)^2} = 250\pi \) (cm2).
Diện tích vải cần để làm chiếc mũ là:
S = S1 + S2 = 225π + 250π = 475π ≈ 1492,2 (cm2).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
R = 2 : 2 = 1 cm.
Thể tích của một viên bi là: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.1^3} = \frac{4}{3}\pi \) (cm3).
Thể tích của năm viên bi là: \(5.\frac{4}{3}\pi = \frac{{20}}{3}\pi \) (cm3).
Vì thể tích lượng nước tràn ra khỏi cốc bằng thể tích của năm viên bi nên lượng nước tràn ra khỏi cốc là \(\frac{{20}}{3}\pi \approx 21\) cm3 nước.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
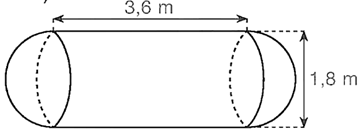
Thể tích bồn chứa xăng là:
\(\pi .{\left( {\frac{{1,8}}{2}} \right)^2}.3,6 + \frac{4}{3}\pi .{\left( {\frac{{1,8}}{2}} \right)^3} = \frac{{486}}{{125}}\pi \approx 12,21\) (m3).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Nếu làm theo cách 1 thì chu vi đường tròn đáy là: 240 cm, \({R_1} = \frac{{240}}{{2\pi }} = \frac{{120}}{\pi }\) (cm).
Nếu làm theo cách 2 thì chu vi của mỗi đường tròn đáy là \(\frac{{240}}{2} = 120\) cm, \({R_2} = \frac{{120}}{{2\pi }} = \frac{{60}}{\pi }\) (cm).
Ta có: \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\pi {R_1}^2h}}{{2\pi {R_2}^2h}} = \frac{{{R_1}^2}}{{2{R_2}^2}} = \frac{1}{2}{\left( {\frac{{{R_1}}}{{{R_2}}}} \right)^2} = \frac{1}{2}{\left( {\frac{{120}}{\pi }:\frac{{60}}{\pi }} \right)^2} = \frac{1}{2}{.2^2} = 2.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 1/7 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập