Giải VTH Toán 9 KNTT Bài 14. Cung và dây của một đường tròn có đáp án

Đáp án đúng là: D

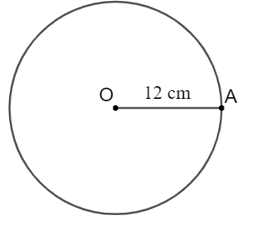
Dây có độ dài lớn nhất của đường tròn là đường kính.

Đường kính của đường tròn (O; 12 cm) là 12 . 2 = 24 (cm).

Vậy dây lớn nhất nhất của đường tròn (O; 12 cm) có độ dài bằng 24 cm.

Đáp án đúng là: B

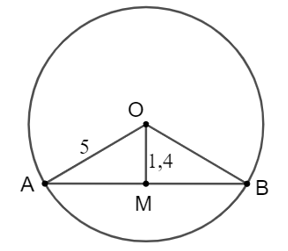
Xét đường tròn (O) có: OA = OB suy ra tam giác OAB là tam giác cân tại O.

Vì M là trung điểm của AB mà tam giác OAB cân tại O suy ra OM vừa là đường trung tuyến vừa là đường cao.

Xét tam giác OAM vuông tại M, áp dụng định lí Pythagore, ta có:

\(A{M^2} = O{A^2} - O{M^2} = {5^2} - {1,4^2} = 23,04\) nên \(AM = \sqrt {23,04} = 4,8\) (cm).

Vì M là trung điểm của AB nên \(AM = BM = \frac{{AB}}{2} = 4,8.\)

Suy ra AB = 2AM = 9,6 cm.

Vậy độ dài dây AB là 9,6 cm.

Đáp án đúng là: A

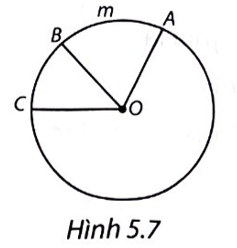
Xét đường tròn (O), ta có cung AmB bị chắn bởi góc ở tâm AOB, góc ở tâm AOC chắn cung AC.

Vậy khẳng định A là khẳng định đúng.

Đáp án đúng là: B

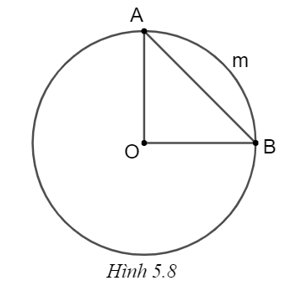
Xét đường tròn (O), ta có số đo ở cung AmB bằng số đo góc \(\widehat {AOB}.\)

Ta có OA = OB = R và \(AB = \sqrt 2 R\)

Mà \[O{A^2} + O{B^2} = 2{R^2} = A{B^2}\] nên tam giác OAB là tam giác vuông cân (định lí Pythagore đảo).

Do đó

Vậy số đo của cung AmB là 90°.

(H.5.9)

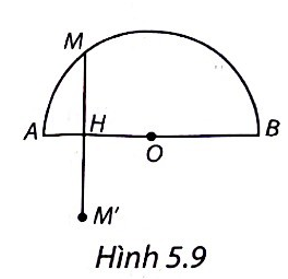
Gọi H là chân đường cao hạ từ M xuống AB.

Khi đó, độ dài đoạn MH là khoảng cách từ M đến AB.

Gọi M' là điểm đối xứng với M qua AB. Khi đó, H là trung điểm của MM', tức là MH = HM'.

Mặt khác, do AB là đường kính của đường tròn nên M' thuộc đường tròn (O).

Suy ra MM' là dây cung của đường tròn.

Do đó \[MM' \le AB,\] hay 2MH ≤ AB, suy ra \(MH \le \frac{{AB}}{2}.\)

Vậy khoảng cách từ M đến AB không lớn hơn \(\frac{{AB}}{2}.\)

(H.5.10)

Theo giả thiết, ta có OA = OB = 5 cm; AB = 6 cm.

a) Gọi C là trung điểm của AB, ta có AC = BC = 3 cm.

Trong tam giác OAB cân tại O (OA = OB) có OC là đường trung tuyến nên cũng là đường cao, nghĩa là OC ⊥ AB.

Do đó, OC là khoảng cách từ O đến đường thẳng AB.

Trong tam giác vuông AOC, ta có:

\(O{C^2} = O{A^2} - A{C^2} = {5^2} - {3^2} = 16,\) suy ra \[OC = \sqrt {16} = 4\] cm.

Vậy khoảng cách từ O đến đường thẳng AB là 4 cm.

b) Trong tam giác cân OAB, đường trung tuyến OC cũng là đường phân giác, mà \(\widehat {AOB} = 2\alpha \) nên \(\widehat {AOC} = \frac{1}{2}\widehat {AOB} = \alpha .\)

Xét tam giác AOC vuông tại C, ta có: \(\tan \alpha = \tan \widehat {AOC} = \frac{{AC}}{{OC}} = \frac{3}{4}.\)