Chọn phương án đúng.
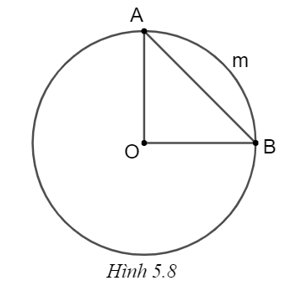
Cho đường tròn (O; R), vẽ dây \(AB = \sqrt 2 R\) (H.5.8). Số đo của cung AmB là
A. 45°.
B. 90°.
C. 270°.
D. 60°.
Chọn phương án đúng.
Cho đường tròn (O; R), vẽ dây \(AB = \sqrt 2 R\) (H.5.8). Số đo của cung AmB là
A. 45°.
B. 90°.
C. 270°.
D. 60°.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Xét đường tròn (O), ta có số đo ở cung AmB bằng số đo góc \(\widehat {AOB}.\)
Ta có OA = OB = R và \(AB = \sqrt 2 R\)
Mà \[O{A^2} + O{B^2} = 2{R^2} = A{B^2}\] nên tam giác OAB là tam giác vuông cân (định lí Pythagore đảo).
Do đó
Vậy số đo của cung AmB là 90°.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(H.5.10)
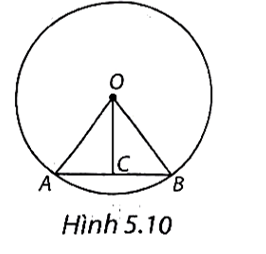
Theo giả thiết, ta có OA = OB = 5 cm; AB = 6 cm.
a) Gọi C là trung điểm của AB, ta có AC = BC = 3 cm.
Trong tam giác OAB cân tại O (OA = OB) có OC là đường trung tuyến nên cũng là đường cao, nghĩa là OC ⊥ AB.
Do đó, OC là khoảng cách từ O đến đường thẳng AB.
Trong tam giác vuông AOC, ta có:
\(O{C^2} = O{A^2} - A{C^2} = {5^2} - {3^2} = 16,\) suy ra \[OC = \sqrt {16} = 4\] cm.
Vậy khoảng cách từ O đến đường thẳng AB là 4 cm.
b) Trong tam giác cân OAB, đường trung tuyến OC cũng là đường phân giác, mà \(\widehat {AOB} = 2\alpha \) nên \(\widehat {AOC} = \frac{1}{2}\widehat {AOB} = \alpha .\)
Xét tam giác AOC vuông tại C, ta có: \(\tan \alpha = \tan \widehat {AOC} = \frac{{AC}}{{OC}} = \frac{3}{4}.\)
Lời giải
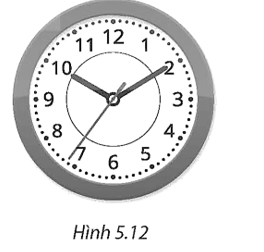
a) Trong 1 giờ (60 phút), đầu kim phút vạch nên cả vòng tròn 360°.
Do đó trong 36 phút, đầu kim phút vạch một cung có số đo là
\(\frac{{36}}{{60}}.360^\circ = 216^\circ .\)
b) Trong 12 giờ (720 phút), đầu kim giờ vạch nên cả vòng tròn 360°.
Do đó trong 36 phút, đầu kim giờ vạch nên một cung có số đo là
\(\frac{{36}}{{720}}.360^\circ = 18^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo