Giải VTH Toán 9 KNTT Luyện tập chung có đáp án
34 người thi tuần này 4.6 385 lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
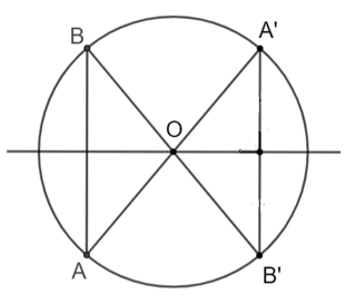
Do tính đối xứng tâm của (O) nên A' và B' cũng thuộc (O).
Do đó OA = OB = OA' = OB', suy ra đường trung trực của A'B' đi qua O.
Vậy đường trung trực của A'B' là trục đối xứng của (O).
Lời giải
(H.5.20)
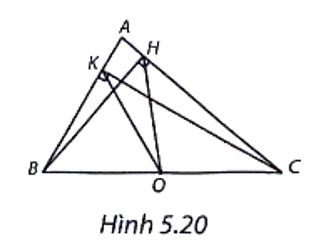
a) Gọi O là trung điểm của BC.
Do \(\widehat {BHC} = \widehat {BKC} = 90^\circ \) nên trong các tam giác BHC và BKC có đường trung tuyến bằng \(\frac{1}{2}\) cạnh huyền.
Ta có: \(OH = OK = OB = OC = \frac{{BC}}{2}.\)
Do đó, đường tròn đường kính BC đi qua các điểm H và K.
b) Theo câu a, HK là dây cung của đường tròn đường kính BC. Do đó KH < BC.
Lời giải
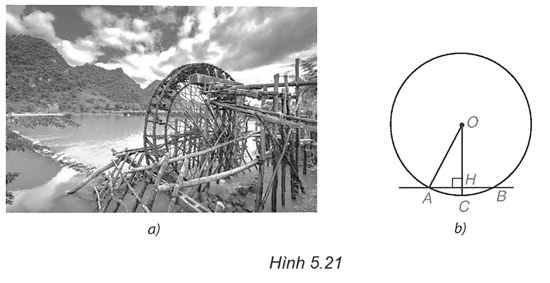
Gọi R (m) là bán kính của guồng nước.
Trên hình vẽ, ta thấy OH = R – HC = R – 0,5 (m).
Do OH < AB nên \(HA = HB = \frac{{AB}}{2} = 2\) m.
Trong tam giác vuông AOH, theo định lí Pythagore ta có:
\(O{A^2} = O{H^2} + H{A^2} = {\left( {R - 0,5} \right)^2} + {2^2}.\)
Tức là \(O{A^2} = {R^2} - R + 0,25 + 4 = {R^2} - R + 4,25.\)
Từ đó suy ra \({R^2} = {R^2} - R + 4,25,\) hay 4,25 – R = 0. Do đó, R = 4,25 m.
Vậy bán kính của guồng nước là 4,25 m.
Lời giải
a) Vẽ dây AB cách O một khoảng 2,5 cm:
− Lấy điểm I tùy ý sao cho OI = 2,5 cm;
− Vẽ đường thẳng vuông góc với OI tại I, cắt (O) tại A và B.
Ta có dây AB cần vẽ:
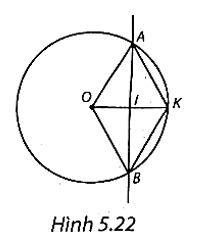
b) (H.5.22) Trong tam giác vuông AOI, ta có AI2 = OA2 – OI2 = 52 – 2,52 = 18,75.
Vậy \(AB = 2AI = 2\sqrt {18,75} = 5\sqrt 3 \approx 8,66\) cm.
c) (H.5.22)
• Kéo dài OI cắt (O) tại K.
Dễ thấy tứ giác AKBO có hai đường chéo AB và OK vuông góc với nhau và cắt nhau tại trung điểm mỗi đường (do OK = OA = 5 cm và \(OI = IK = \frac{{OK}}{2}).\)
Do đó AKBO là hình thoi.
Từ đó OA = OK = KA = 5 cm; OAK là tam giác đều, suy ra \(\widehat {AOK} = 60^\circ \) và \(\widehat {AOB} = 2\widehat {AOK} = 2.60^\circ = 120^\circ .\)
Vậy
• Độ dài cung nhỏ AB bằng \(\frac{{120}}{{180}}\pi .5 = \frac{{10\pi }}{3}\) (cm).
d) Diện tích hình quạt tròn ứng với cung AB là \(\frac{{\frac{{10\pi }}{3}.5}}{2} = \frac{{25\pi }}{3}\) (cm2).
Lời giải
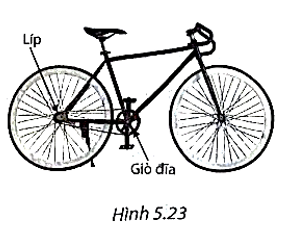
Chu vi của chiếc líp là 2.π.4 = 8π (cm).
Khi người đi xe đạp một vòng thì giò đĩa quay 2π . 15 = 30π (cm).
Mỗi điểm trên xích di chuyển một độ dài đúng bằng chu vi của giò đĩa, tức là 8π cm.
Khi đó, chiếc líp quay được \(\frac{{30\pi }}{{8\pi }} = \frac{{15}}{4}\) vòng, nghĩa là bánh xe quay được \(\frac{{15}}{4}\) vòng.
Chu vi của bánh xe (đường kính 65 cm = 0,65 m) là 0,65π (m).
Do đó quãng đường xe di chuyển được khi bánh xe quay \(\frac{{15}}{4}\) vòng là:
\(0,65\pi .\frac{{15}}{4} = \frac{{39\pi }}{{16}} \approx 7,7\) (m)
Vậy khi người đi xe đạp một vòng thì xe di chuyển được quãng đường khoảng 7,7 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.