Câu hỏi:
17/09/2024 284
Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng:
a) Đường tròn đường kính BC đi qua các điểm H và K;
b) KH < BC.
Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng:
a) Đường tròn đường kính BC đi qua các điểm H và K;
b) KH < BC.
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Luyện tập chung có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
(H.5.20)
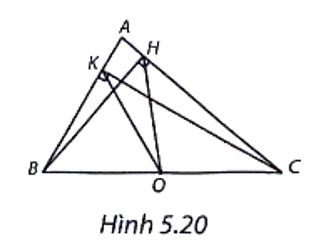
a) Gọi O là trung điểm của BC.
Do \(\widehat {BHC} = \widehat {BKC} = 90^\circ \) nên trong các tam giác BHC và BKC có đường trung tuyến bằng \(\frac{1}{2}\) cạnh huyền.
Ta có: \(OH = OK = OB = OC = \frac{{BC}}{2}.\)
Do đó, đường tròn đường kính BC đi qua các điểm H và K.
b) Theo câu a, HK là dây cung của đường tròn đường kính BC. Do đó KH < BC.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
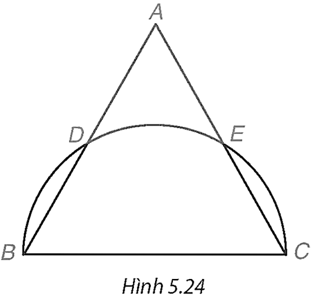
(H.5.25)
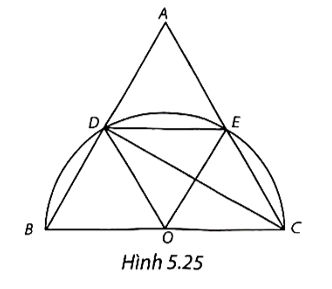
a) Gọi O là trung điểm của BC.
Tam giác DBC có đường trung tuyến OD bằng OB và OC (bằng \(\frac{1}{2}BC\)) nên DBC là tam giác vuông tại D.
Do đó, CD là đường cao của tam giác đều ABC, suy ra D là trung điểm của AB.
Tương tự, E là trung điểm của AC.
Từ đó suy ra bốn tam giác ADE, OEC, OBD, ODE là những tam giác đều, với độ dài cạnh bằng một nửa cạnh của tam giác đều ABC, tức là bằng \(\frac{{2\sqrt 3 }}{2} = \sqrt 3 \) cm.
Ba cung nhỏ và lần lượt bị chắn bởi các góc ở tâm \(\widehat {BOD},\) \(\widehat {DOE}\) và \(\widehat {EOC}\) mà các góc này đều bằng 60° (các góc của tam giác đều) nên các cung đang xét đều bằng nhau và cùng có số đo bằng 60°.
b) Diện tích hình quạt tròn ứng với cung BD là
\({S_q} = \frac{{60}}{{360}}\pi {\left( {\sqrt 3 } \right)^2} = \frac{\pi }{2}\) (cm2).
Diện tích của tam giác BOD là
\({S_{BOD}} = \frac{1}{2}{\left( {\sqrt 3 } \right)^2}.\sin 60^\circ = \frac{{3\sqrt 3 }}{4}\) (cm2).
Diện tích của hình viên phân là
\(S = {S_q} - {S_{BOD}} = \frac{\pi }{2} - \frac{{3\sqrt 3 }}{4} \approx 0,27\) (cm2).
Lời giải
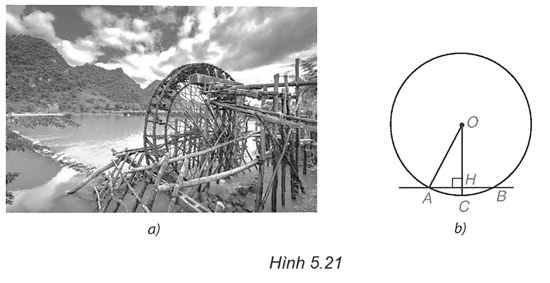
a) Vẽ dây AB cách O một khoảng 2,5 cm:
− Lấy điểm I tùy ý sao cho OI = 2,5 cm;
− Vẽ đường thẳng vuông góc với OI tại I, cắt (O) tại A và B.
Ta có dây AB cần vẽ:
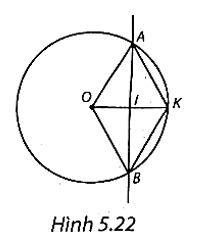
b) (H.5.22) Trong tam giác vuông AOI, ta có AI2 = OA2 – OI2 = 52 – 2,52 = 18,75.
Vậy \(AB = 2AI = 2\sqrt {18,75} = 5\sqrt 3 \approx 8,66\) cm.
c) (H.5.22)
• Kéo dài OI cắt (O) tại K.
Dễ thấy tứ giác AKBO có hai đường chéo AB và OK vuông góc với nhau và cắt nhau tại trung điểm mỗi đường (do OK = OA = 5 cm và \(OI = IK = \frac{{OK}}{2}).\)
Do đó AKBO là hình thoi.
Từ đó OA = OK = KA = 5 cm; OAK là tam giác đều, suy ra \(\widehat {AOK} = 60^\circ \) và \(\widehat {AOB} = 2\widehat {AOK} = 2.60^\circ = 120^\circ .\)
Vậy
• Độ dài cung nhỏ AB bằng \(\frac{{120}}{{180}}\pi .5 = \frac{{10\pi }}{3}\) (cm).
d) Diện tích hình quạt tròn ứng với cung AB là \(\frac{{\frac{{10\pi }}{3}.5}}{2} = \frac{{25\pi }}{3}\) (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận