Giải SBT Toán 9 KNTT Bài 21. Giải toán bằng cách lập phương trình có đáp án
32 người thi tuần này 4.6 197 lượt thi 8 câu hỏi
🔥 Đề thi HOT:
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
7.4 K lượt thi
5 câu hỏi
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
29.9 K lượt thi
4 câu hỏi
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
29.9 K lượt thi
3 câu hỏi
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 1. Phương trình quy về phương trình bậc nhất một ẩn có đáp án
1.3 K lượt thi
15 câu hỏi
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
2.1 K lượt thi
12 câu hỏi
Dạng 1. Toán về quan hệ số
3.6 K lượt thi
3 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Diện tích ban đầu của bức ảnh là: 8 . 12 = 96 (cm2)
Gọi độ dài đoạn tăng thêm của mỗi chiều là x (cm) (x > 0).
Diện tích bức ảnh sau khi phóng to là:
(8 + h)(12 + h) = h2 + 20h + 96 (cm2)
Diện tích của bức ảnh sau khi phóng to gấp đôi diện tích bức ảnh ban đầu nên ta có:
h2 + 20h + 96 = 2 . 96
h2 + 20h – 96 = 0
Ta có ∆ = 202 – 4 . 1 . (–96) = 784 > 0 nên phương trình có hai nghiệm phân biệt:
(thỏa mãn điều kiện);
(không thỏa mãn điều kiện).
Do đó người ta đã tăng mỗi chiều của bức ảnh thêm 4 cm.
Chiều dài bức ảnh mới là: 12 + 4 = 16 (cm)
Chiều rộng bức ảnh mới là: 8 + 4 = 12 (cm)
Vậy chiều dài và chiều rộng bức ảnh mới lần lượt là 16 cm và 12 cm.
Lời giải
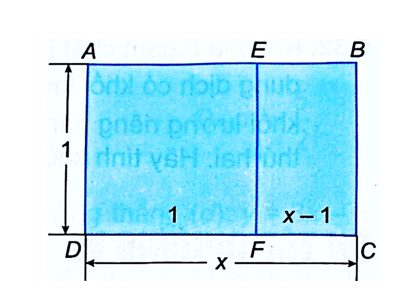
a) Theo hình vẽ, ta thấy tỉ lệ giữa chiều dài và chiều rộng hình chữ nhật ABCD là:
.
Tỉ lệ giữa chiều dài và chiều rộng hình chữ nhật EBCF là:
.
b) Theo đề bài, ta có:
x(x – 1) = 1
x2 – x = 1
x2 – x – 1 = 0
Ta có: ∆ = (–1)2 – 4 . 1 . (–1) = 5 > 0 nên phương trình có hai nghiệm phân biệt:
(thỏa mãn);
(không thỏa mãn).
Vậy tỉ lệ vàng là .
Lời giải
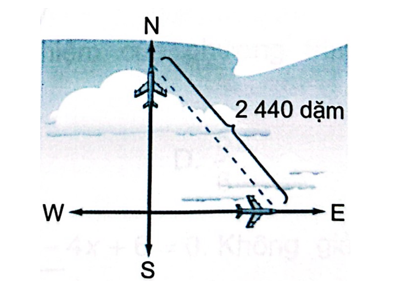
Gọi vận tốc chiếc máy bay đang bay về hướng đông là x (dặm/giờ) (x > 0).
Do đó vận tốc chiếc máy bay đang bay về hướng bắc là x + 50 (dặm/giờ).
Sau 3 giờ hai chiếc máy bay cách nhau 2 440 dặm nên ta có:
(3x)2 + [3(x + 50)]2 = 2 4402
18x2 + 900x – 22 500 = 5 953 600
18x2 + 900x – 5 931 100 = 0
9x2 + 450x – 2 965 550 = 0
Ta có: ∆ = 4502 – 4 . 9 . (–2 965 550) = 106 962 300 > 0 nên phương trình có hai nghiệm phân biệt:
(thỏa mãn điều kiện)
(không thỏa mãn điều kiện)
Do đó vận tốc của chiếc máy bay đang bay về hướng đông xấp xỉ bằng 549,57 dặm/giờ.
Vận tốc của chiếc máy bay đang bay về hướng bắc xấp xỉ bằng:
549,57 + 50 = 599,57 (dặm/giờ).
Vậy vận tốc của chiếc máy bay đang bay về hướng đông xấp xỉ bằng 549,57 dặm/giờ và vận tốc của chiếc máy bay đang bay về hướng bắc xấp xỉ bằng 599,57 dặm/giờ.
Lời giải
Gọi số dãy ghế trong phòng họp lúc đầu là x (dãy) ().
Số chỗ ngồi ở mỗi dãy ghế lúc đầu là (chỗ).
Số chỗ ngồi ở mỗi dãy ghế sau khi xếp thêm là (chỗ).
Mỗi dãy ghế tăng thêm 1 chỗ ngồi nên ta có phương trình:
55x – 40(x + 1) = x(x + 1)
15x – 40 = x2 + x
x2 – 14x + 40 = 0
Ta có ∆ = (–14)2 – 4 . 1 . 40 = 36 > 0 nên phương trình có hai nghiệm phân biệt:
(thỏa mãn);
(thỏa mãn).
Vậy có 2 trường hợp cho phòng họp lúc đầu là có 4 dãy ghế, mỗi dãy có 10 chỗ ngồi và có 10 dãy ghế, mỗi dãy có 4 chỗ ngồi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo