Hình chữ nhật vàng là hình chữ nhật có thể chia thành một hình vuông và hình chữ nhật thứ hai có các kích thước tỉ lệ với các kích thước tương ứng của hình chữ nhật ban đầu (với cùng hệ số tỉ lệ). Tỉ số x giữa chiều dài và chiều rộng của hình chữ nhật vàng được gọi là tỉ lệ vàng.
a) Tìm tỉ số giữa chiều dài và chiều rộng của hình chữ nhật ABCD và hình chữ nhật EBCF.
b) Tìm giá trị chính xác của tỉ lệ vàng bằng cách đặt hai tỉ số ở câu a bằng nhau rồi tìm x.
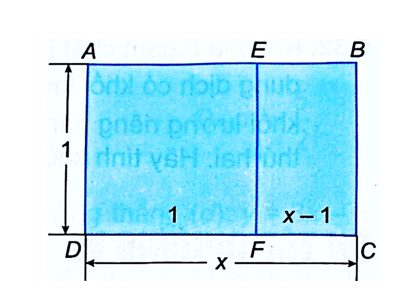
Hình chữ nhật vàng là hình chữ nhật có thể chia thành một hình vuông và hình chữ nhật thứ hai có các kích thước tỉ lệ với các kích thước tương ứng của hình chữ nhật ban đầu (với cùng hệ số tỉ lệ). Tỉ số x giữa chiều dài và chiều rộng của hình chữ nhật vàng được gọi là tỉ lệ vàng.
a) Tìm tỉ số giữa chiều dài và chiều rộng của hình chữ nhật ABCD và hình chữ nhật EBCF.
b) Tìm giá trị chính xác của tỉ lệ vàng bằng cách đặt hai tỉ số ở câu a bằng nhau rồi tìm x.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Theo hình vẽ, ta thấy tỉ lệ giữa chiều dài và chiều rộng hình chữ nhật ABCD là:
.
Tỉ lệ giữa chiều dài và chiều rộng hình chữ nhật EBCF là:
.
b) Theo đề bài, ta có:
x(x – 1) = 1
x2 – x = 1
x2 – x – 1 = 0
Ta có: ∆ = (–1)2 – 4 . 1 . (–1) = 5 > 0 nên phương trình có hai nghiệm phân biệt:
(thỏa mãn);
(không thỏa mãn).
Vậy tỉ lệ vàng là .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đổi 16 phút = giờ.
Gọi vận tốc của xe máy đi từ A đến B là x (km/h) (x > 0).
Vận tốc của ô tô đi từ B về A là x + 15 (km/h).
Hai xe gặp nhau ở địa điểm cách B 24 km nên ô tô đã đi được 24 km.
Quãng đường xe máy đã đi được là: 54 – 24 = 30 (km)
Thời gian ô tô đã đi là giờ.
Thời gian xe máy đã đi là giờ.
Xe máy đi nhiều hơn ô tô 16 phút ( giờ) nên ta có phương trình:
15(6x + 450) = 4x(x + 15)
90x + 6 750 = 4x2 + 60x
4x2 – 30x – 6 750 = 0
2x2 – 15x – 3 375 = 0
Ta có: ∆ = (–15)2 – 4 . 2 . (–3 375) = 27 225 > 0 nên phương trình có hai nghiệm phân biệt:
(thỏa mãn điều kiện);
(không thỏa mãn điều kiện)
Vậy vận tốc của xe máy là 45 km/h và vận tốc của ô tô là 45 + 15 = 60 (km/h).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Diện tích ban đầu của bức ảnh là: 8 . 12 = 96 (cm2)
Gọi độ dài đoạn tăng thêm của mỗi chiều là x (cm) (x > 0).
Diện tích bức ảnh sau khi phóng to là:
(8 + h)(12 + h) = h2 + 20h + 96 (cm2)
Diện tích của bức ảnh sau khi phóng to gấp đôi diện tích bức ảnh ban đầu nên ta có:
h2 + 20h + 96 = 2 . 96
h2 + 20h – 96 = 0
Ta có ∆ = 202 – 4 . 1 . (–96) = 784 > 0 nên phương trình có hai nghiệm phân biệt:
(thỏa mãn điều kiện);
(không thỏa mãn điều kiện).
Do đó người ta đã tăng mỗi chiều của bức ảnh thêm 4 cm.
Chiều dài bức ảnh mới là: 12 + 4 = 16 (cm)
Chiều rộng bức ảnh mới là: 8 + 4 = 12 (cm)
Vậy chiều dài và chiều rộng bức ảnh mới lần lượt là 16 cm và 12 cm.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập