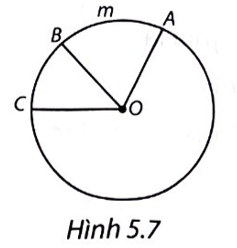
Trên mặt một chiếc đồng hồ có các vạch chia như Hình 5.12. Hỏi cứ sau mỗi khoảng thời gian 36 phút:
a) Đầu kim phút vạch nên một cung có số đo bằng bao nhiêu độ?
b) Đầu kim giờ vạch nên một cung có số đo bằng bao nhiêu độ?
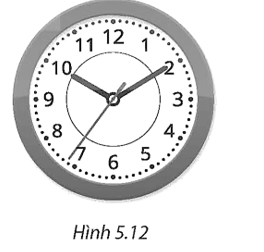
Trên mặt một chiếc đồng hồ có các vạch chia như Hình 5.12. Hỏi cứ sau mỗi khoảng thời gian 36 phút:
a) Đầu kim phút vạch nên một cung có số đo bằng bao nhiêu độ?
b) Đầu kim giờ vạch nên một cung có số đo bằng bao nhiêu độ?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Trong 1 giờ (60 phút), đầu kim phút vạch nên cả vòng tròn 360°.
Do đó trong 36 phút, đầu kim phút vạch một cung có số đo là
\(\frac{{36}}{{60}}.360^\circ = 216^\circ .\)
b) Trong 12 giờ (720 phút), đầu kim giờ vạch nên cả vòng tròn 360°.
Do đó trong 36 phút, đầu kim giờ vạch nên một cung có số đo là
\(\frac{{36}}{{720}}.360^\circ = 18^\circ .\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
(H.5.10)
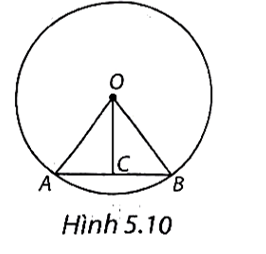
Theo giả thiết, ta có OA = OB = 5 cm; AB = 6 cm.
a) Gọi C là trung điểm của AB, ta có AC = BC = 3 cm.
Trong tam giác OAB cân tại O (OA = OB) có OC là đường trung tuyến nên cũng là đường cao, nghĩa là OC ⊥ AB.
Do đó, OC là khoảng cách từ O đến đường thẳng AB.
Trong tam giác vuông AOC, ta có:
\(O{C^2} = O{A^2} - A{C^2} = {5^2} - {3^2} = 16,\) suy ra \[OC = \sqrt {16} = 4\] cm.
Vậy khoảng cách từ O đến đường thẳng AB là 4 cm.
b) Trong tam giác cân OAB, đường trung tuyến OC cũng là đường phân giác, mà \(\widehat {AOB} = 2\alpha \) nên \(\widehat {AOC} = \frac{1}{2}\widehat {AOB} = \alpha .\)
Xét tam giác AOC vuông tại C, ta có: \(\tan \alpha = \tan \widehat {AOC} = \frac{{AC}}{{OC}} = \frac{3}{4}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
(H.5.11)
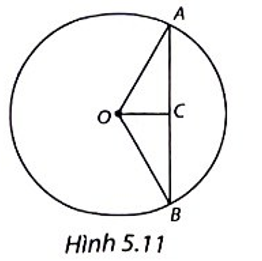
Gọi C là trung điểm của AB.
Chứng minh tương tự bài tập 2, ta suy ra OC là khoảng cách từ O đến AB.
Theo đề bài, ta có OC = 3 cm và
Do OC vừa là đường trung tuyến vừa là đường phân giác nên \(\widehat {AOC} = \frac{1}{2}\widehat {AOB} = 50^\circ .\)
Trong tam giác vuông AOC, ta có \(\cos \widehat {AOC} = \cos 50^\circ = \frac{{OC}}{{OA}}.\)
Vậy bán kính đường tròn (O) là
\(R = OA = \frac{{OC}}{{\cos 50^\circ }} = \frac{3}{{\cos 50^\circ }} \approx 4,7\) (cm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập