Câu hỏi:
28/08/2024 5,916
Chiếc mũ của chú hề với các kích thước như hình bên. Hãy tính tổng diện tích vải cần để làm nên chiếc mũ (coi mép khâu không đáng kể và làm tròn kết quả đến hàng phần mười của cm2).
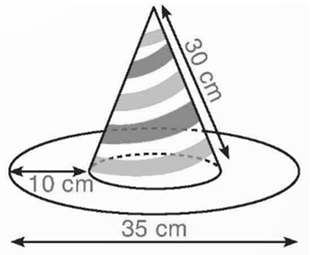
Chiếc mũ của chú hề với các kích thước như hình bên. Hãy tính tổng diện tích vải cần để làm nên chiếc mũ (coi mép khâu không đáng kể và làm tròn kết quả đến hàng phần mười của cm2).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Bán kính đường tròn đáy của hình nón là
(35 – 10.2) : 2 = 7,5 (cm).
Diện tích xung quanh của hình nón là:
S1 = πRl = π.7,5.30 = 225π (cm2).
Diện tích phần vành mũ (hình vành khăn) là:
\({S_2} = \pi .{\left( {17,5} \right)^2} - \pi .{\left( {7,5} \right)^2} = 250\pi \) (cm2).
Diện tích vải cần để làm chiếc mũ là:
S = S1 + S2 = 225π + 250π = 475π ≈ 1492,2 (cm2).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
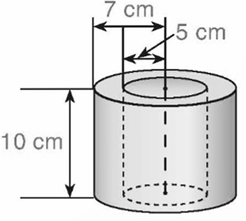
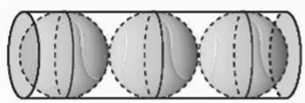
R = 2 : 2 = 1 cm.
Thể tích của một viên bi là: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.1^3} = \frac{4}{3}\pi \) (cm3).
Thể tích của năm viên bi là: \(5.\frac{4}{3}\pi = \frac{{20}}{3}\pi \) (cm3).
Vì thể tích lượng nước tràn ra khỏi cốc bằng thể tích của năm viên bi nên lượng nước tràn ra khỏi cốc là \(\frac{{20}}{3}\pi \approx 21\) cm3 nước.
Lời giải
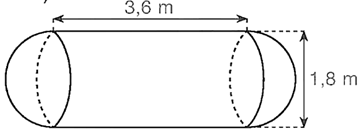
Thể tích bồn chứa xăng là:
\(\pi .{\left( {\frac{{1,8}}{2}} \right)^2}.3,6 + \frac{4}{3}\pi .{\left( {\frac{{1,8}}{2}} \right)^3} = \frac{{486}}{{125}}\pi \approx 12,21\) (m3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
Nhắn tin Zalo