Câu hỏi:
13/07/2024 6,746
Một đội xe gồm các xe tải cùng loại, cần phải chở 120 tấn hàng. Tuy nhiên khi làm việc, có hai xe phải điều chuyển đi nơi khác nên mỗi xe phải chở thêm 3 tấn hàng. Hỏi đội xe đó có bao nhiêu chiếc xe tải?
Một đội xe gồm các xe tải cùng loại, cần phải chở 120 tấn hàng. Tuy nhiên khi làm việc, có hai xe phải điều chuyển đi nơi khác nên mỗi xe phải chở thêm 3 tấn hàng. Hỏi đội xe đó có bao nhiêu chiếc xe tải?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi x (chiếc) là số xe tải của đội xe (x ∈ ℕ, x > 2).
Số tấn hàng mỗi xe cần chở là: 
(tấn).
Số xe tải còn lại sau khi điều chuyển hai xe đi nơi khác là: x – 2 (chiếc).
Lúc này, số tấn hàng mỗi xe phải chở là: 
(tấn).
Theo bài, khi làm việc có hai xe phải điều chuyển đi nơi khác nên mỗi xe phải chở thêm 3 tấn hàng nên ta có phương trình:
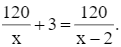
Quy đồng mẫu hai vế của phương trình, ta được:
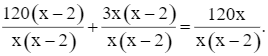
Nhân cả hai vế của phương trình với x(x – 2) để khử mẫu, ta được phương trình:
120(x – 2) + 3x(x – 2) = 120x
120x – 240 + 3x2 – 6x – 120x = 0
3x2 – 6x – 240 = 0
x2 – 2x – 80 = 0
Ta có ∆’ = (–1)2 – 1.(–80) = 81 > 0 và 
Suy ra phương trình trên có hai nghiệm phân biệt:
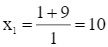(thỏa mãn điều kiện); 
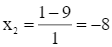(loại).
Vậy đội xe đó có 10 chiếc xe tải.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x (chiếc) là số áo phải may trong 1 ngày theo kế hoạch (x ∈ ℕ, x > 0).
Số áo thực tế xưởng đã may trong 1 ngày là x + 10 (chiếc).
Thời gian may 1 500 chiếc áo là: 
(ngày).
Thời gian may 1 320 chiếc áo là: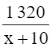 
(ngày).
Theo bài, xưởng hoàn thành sớm 3 ngày so với kế hoạch nên ta có phương trình: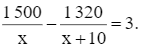 
Quy đồng mẫu vế trái của phương trình, ta được:
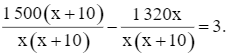
Nhân hai vế của phương trình với x(x + 10) để khử mẫu, ta được phương trình:
1 500(x + 10) – 1 320x = 3x(x + 10)
1 500x + 15 000 – 1 320x = 3x2 + 30x
3x2 – 150x – 15 000 = 0
x2 – 50x – 5 000 = 0.
Ta có ∆’ = (–25)2 – 1.(–5 000) = 5 625 và 
Suy ra phương trình có hai nghiệm phân biệt:
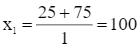(thỏa mãn điều kiện); 
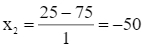(loại).
Vậy theo kế hoạch mỗi ngày xưởng may 100 chiếc áo.
Lời giải
Gọi x là lãi suất gửi tiết kiệm của bác Lan (x được cho dưới dạng số thập phân) (x > 0).
Số tiền thu được (cả vốn lẫn lãi) của bác Lan sau kì gửi thứ nhất là:
100(1 + x) (triệu đồng).
Số tiền thu được (cả vốn lẫn lãi) của bác Lan sau kì gửi thứ nhất là:
100(1 + x)(1 + x) = 100(1 + x)2 (triệu đồng).
Theo bài, sau hai năm bác Lan rút tiền ra thì nhận được 118,81 triệu đồng cả vốn lẫn lãi nên ta có phương trình:
100(1 + x)2 = 118,81
(1 + x)2 = 1,1881
1 + x = 1,09 (do x > 0).
x = 0,09.
Vậy lãi suất gửi tiết kiệm là 9%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận