Sau hai năm, số dân của một thành phố tăng từ 1 200 000 người lên 1 452 000 người. Hỏi trung bình mỗi năm dân số của thành phố đó tăng bao nhiêu phần trăm?
Sau hai năm, số dân của một thành phố tăng từ 1 200 000 người lên 1 452 000 người. Hỏi trung bình mỗi năm dân số của thành phố đó tăng bao nhiêu phần trăm?
Quảng cáo
Trả lời:
Gọi x là tốc độ trung bình tăng dân số của thành phố (x được cho dưới dạng số thập phân, x > 0).
Số dân của thành phố sau năm thứ nhất là: 1 200 000.(1 + x) (người).
Số dân của thành phố sau năm thứ hai là:
1 200 000.(1 + x).(1 + x) = 1 200 000.(1 + x)2 (người).
Theo bài, ta có phương trình:
1 200 000.(1 + x)2 = 1 452 000
(1 + x)2 = 1,21
1 + x = 1,1 (do x > 0).
x = 0,1 (thỏa mãn).
Vậy tốc độ gia tăng dân số của thành phố đó là 0,1 = 10%.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x (chiếc) là số áo phải may trong 1 ngày theo kế hoạch (x ∈ ℕ, x > 0).
Số áo thực tế xưởng đã may trong 1 ngày là x + 10 (chiếc).
Thời gian may 1 500 chiếc áo là: ![]() (ngày).
(ngày).
Thời gian may 1 320 chiếc áo là: 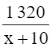 (ngày).
(ngày).
Theo bài, xưởng hoàn thành sớm 3 ngày so với kế hoạch nên ta có phương trình: 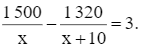
Quy đồng mẫu vế trái của phương trình, ta được:
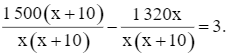
Nhân hai vế của phương trình với x(x + 10) để khử mẫu, ta được phương trình:
1 500(x + 10) – 1 320x = 3x(x + 10)
1 500x + 15 000 – 1 320x = 3x2 + 30x
3x2 – 150x – 15 000 = 0
x2 – 50x – 5 000 = 0.
Ta có ∆’ = (–25)2 – 1.(–5 000) = 5 625 và ![]()
Suy ra phương trình có hai nghiệm phân biệt:
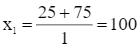 (thỏa mãn điều kiện);
(thỏa mãn điều kiện); 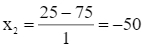 (loại).
(loại).
Vậy theo kế hoạch mỗi ngày xưởng may 100 chiếc áo.
Lời giải
Gọi x là lãi suất gửi tiết kiệm của bác Lan (x được cho dưới dạng số thập phân) (x > 0).
Số tiền thu được (cả vốn lẫn lãi) của bác Lan sau kì gửi thứ nhất là:
100(1 + x) (triệu đồng).
Số tiền thu được (cả vốn lẫn lãi) của bác Lan sau kì gửi thứ nhất là:
100(1 + x)(1 + x) = 100(1 + x)2 (triệu đồng).
Theo bài, sau hai năm bác Lan rút tiền ra thì nhận được 118,81 triệu đồng cả vốn lẫn lãi nên ta có phương trình:
100(1 + x)2 = 118,81
(1 + x)2 = 1,1881
1 + x = 1,09 (do x > 0).
x = 0,09.
Vậy lãi suất gửi tiết kiệm là 9%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.