Một công ty du lịch ghi lại độ tuổi các du khách đặt một tour du lịch mạo hiểm ở bảng sau:
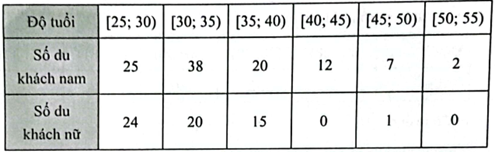
a) Hãy so sánh độ phân tán của độ tuổi du khách nam và du khách nữ theo khoảng biến thiên và khoảng tứ phân vị.
b) Biết rằng trong mẫu số liệu trên có một du khách nữ 49 tuổi. Hỏi độ tuổi của du khách nữ đó có là giá trị ngoại lệ khi so với độ tuổi của các du khách nữ không?
Một công ty du lịch ghi lại độ tuổi các du khách đặt một tour du lịch mạo hiểm ở bảng sau:

a) Hãy so sánh độ phân tán của độ tuổi du khách nam và du khách nữ theo khoảng biến thiên và khoảng tứ phân vị.
b) Biết rằng trong mẫu số liệu trên có một du khách nữ 49 tuổi. Hỏi độ tuổi của du khách nữ đó có là giá trị ngoại lệ khi so với độ tuổi của các du khách nữ không?
Quảng cáo
Trả lời:
a) Khoảng biến thiên của độ tuổi du khách nam là R1 = 55 – 25 = 30 (tuổi).
Khoảng biến thiên của độ tuổi du khách nữ là R2 = 50 – 25 = 25 (tuổi).
Nếu so sánh theo khoảng biến thiên thì độ tuổi của du khách nam phân tán hơn độ tuổi của du khách nữ.
Đối với mẫu số liệu độ tuổi du khách nam, ta có:
Cỡ mẫu là: n = 25 + 38 + 20 + 12 + 7 + 2 = 104.
Ta có: \(\frac{n}{4} = \frac{{104}}{4} = 26\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là x26 ∈ [30; 35).
Do đó, Q1 = 30 + \(\frac{{26 - 25}}{{38}}\left( {35 - 30} \right)\) = \(\frac{{1145}}{{38}}\).
Ta có: \(\frac{{3n}}{4} = \frac{{3.104}}{4} = 78\).
Tứ phân vị thứ ba của mẫu số liệu gốc là x78 ∈ [35; 40).
Do đó, Q3 = 35 + \(\frac{{78 - \left( {25 + 38} \right)}}{{20}}\left( {40 - 35} \right)\) = \(\frac{{155}}{4}\).
Khoảng tứ phân vị của mẫu số liệu là: ∆Q1 = Q3 – Q1 = \(\frac{{155}}{4}\) − \(\frac{{1145}}{{38}}\) = \(\frac{{655}}{{76}}\) ≈ 8,62.
Đối với mẫu số liệu độ tuổi du khách nữ, ta có:
Cỡ mẫu: n = 24 + 20 + 15 + 0 + 1 + 0 = 60.
Ta có: \(\frac{n}{4} = \frac{{60}}{4} = 15\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là x15 ∈ [25; 30).
Do đó, Q1 = 25 + \(\frac{{15 - 0}}{{24}}\left( {30 - 25} \right)\) = \(\frac{{225}}{8}\).
Ta có: \(\frac{{3n}}{4} = \frac{{3.60}}{4} = 45\).
Tứ phân vị thứ ba của mẫu số liệu gốc là x45 ∈ [35; 40).
Do đó, Q3 = 35 + \(\frac{{45 - \left( {24 + 20} \right)}}{{15}}\left( {40 - 35} \right)\) = \(\frac{{106}}{3}\).
Khoảng tứ phân vị của mẫu số liệu là: ∆Q2 = Q3 – Q1 = \(\frac{{106}}{3}\) − \(\frac{{225}}{8}\) = \(\frac{{173}}{{24}}\) ≈ 7,21.
Nếu so sánh theo khoảng tứ phân vị thì độ tuổi du khách nam phân tán hơn độ tuổi du khách nữ.
b) Với số liệu ghép nhóm của du khách nữ, ta có
Q3 + 1,5∆Q2 = \(\frac{{106}}{3}\) + 1,5.7,21 ≈ 46,15 < 49.
Do đó độ tuổi của nữ du khách đó là giá trị ngoại lệ khi so với độ tuổi của các du khách nữ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
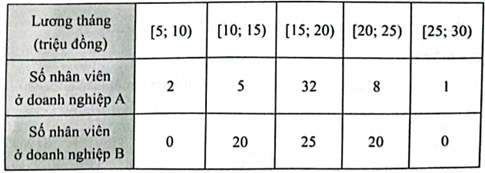
a) Khoảng biến thiên của mức lương ở doanh nghiệp A là RA = 30 – 5 = 25 (triệu đồng).
Khoảng biến thiên của mức lương ở doanh nghiệp B là RB = 25 – 10 = 15 (triệu đồng).
Nếu so sánh theo khoảng biến thiên thì mức lương ở doanh nghiệp A phân tán hơn mức lương ở doanh nghiệp B.
b) Với mẫu số liệu của doanh nghiệp A, ta có:
Cỡ mẫu là: n = 2 + 5 + 32 + 8 + 1 = 48.
Ta có: : \(\frac{n}{4} = \frac{{48}}{4} = 12\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là x12 ∈ [15; 20).
Do đó, Q1 = 15 + \(\frac{{12 - \left( {2 + 5} \right)}}{{32}}\left( {20 - 15} \right)\) = \(\frac{{505}}{{32}}\).
Ta có: \(\frac{{3n}}{4} = \frac{{3.48}}{4} = 36\).
Tứ phân vị thứ ba của mẫu số liệu gốc là x36 ∈ [15; 20).
Do đó, Q3 = 15 + \(\frac{{36 - \left( {2 + 5} \right)}}{{32}}\left( {20 - 15} \right)\) = \(\frac{{625}}{{32}}\).
Vậy khoảng tứ phân vị của mức lương ở doanh nghiệp A là
∆QA = Q3 – Q1 = \(\frac{{625}}{{32}}\) − \(\frac{{505}}{{32}}\) = \(\frac{{15}}{4}\) = 3,75.
Với mẫu số liệu ở doanh nghiệp B, ta có:
Cỡ mẫu là: n = 20 + 25 + 20 = 65.
Ta có: : \(\frac{n}{4} = \frac{{65}}{4} = 16,25\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là x17 ∈ [10; 15).
Do đó, Q1 = 10 + \(\frac{{16,25 - 0}}{{20}}\left( {15 - 10} \right)\) = \(\frac{{225}}{{16}}\).
Ta có: \(\frac{{3n}}{4} = \frac{{3.65}}{4} = 48,75\).
Tứ phân vị thứ ba của mẫu số liệu gốc là x49 ∈ [20; 25).
Do đó, Q3 = 20 + \(\frac{{48,75 - \left( {20 + 25} \right)}}{{20}}\left( {25 - 20} \right)\) = \(\frac{{335}}{{16}}\).
Vậy khoảng tứ phân vị của mức lương ở doanh nghiệp B là
∆QB = Q3 – Q1 = \(\frac{{335}}{{16}}\) − \(\frac{{225}}{{16}}\) = \(\frac{{55}}{8}\) = 6,875.
Vậy nếu so sánh theo khoảng tứ phân vị thì mức lương ở doanh nghiệp B phân tán hơn mức lương ở doanh nghiệp A.
c) Với số liệu ghép nhóm của doanh nghiệp A, ta có:
Q3 + 1,5∆Q = \(\frac{{625}}{{32}}\) + 1,5.3,75 ≈ 25,16 < 27.
Do đó, lương tháng 27 triệu động của nhân viên là giá trị ngoại lê.
Lời giải
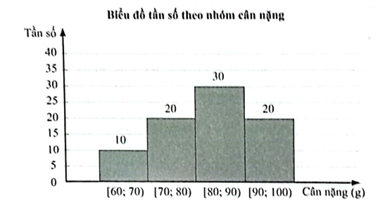
Khoảng biến thiên là: R = 12 – 2 = 10 (giờ).
Cỡ mẫu là: n = 45 + 34 + 23 + 18 + 5 = 125 (người).
Ta có: \(\frac{n}{4} = \frac{{125}}{4} = 31,25\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là x32 ∈ [2; 4).
Do đó, Q1 = 2 + \(\frac{{31,25 - 0}}{{45}}.\left( {4 - 2} \right)\) = \(\frac{{61}}{{18}}\).
Ta có: \(\frac{{3n}}{4} = \frac{{3.125}}{4} = 93,75\).
Tứ phân vị thứ ba của mẫu số liệu gốc là x94 ∈ [6; 8).
Do đó, Q3 = 6 + \(\frac{{93,75 - \left( {45 + 34} \right)}}{{23}}.\left( {8 - 6} \right)\) = \(\frac{{335}}{{46}}\).
Vậy khoảng tứ phân vị của mẫu số liệu là: ∆Q = Q3 – Q1 = \(\frac{{335}}{{46}}\) − \(\frac{{61}}{{18}}\) = \(\frac{{806}}{{207}}\) ≈ 3,89.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.