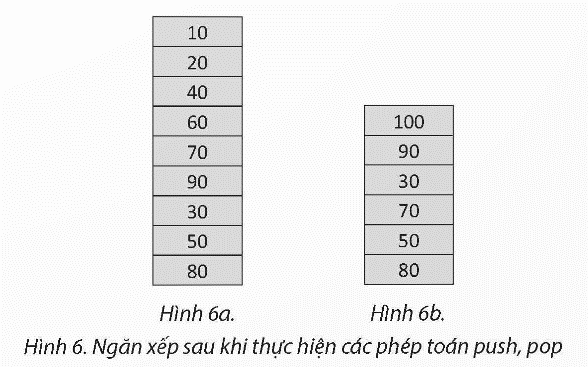
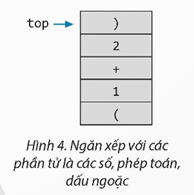
Để tính giá trị một biểu thức số học bằng máy tính, một số nhà khoa học đã sử dụng cách biểu diễn dạng tiền tố (hay còn gọi là kí pháp Ba lan). Ví dụ, biểu thức số học (2-7/3)*(4-1) sẽ được chuyển sang dạng tiền tố có dạng *-2/73-41 (toán tử đặt trước toán hạng) trước khi tính giá trị. Sử dụng các hàm initStack(), push() để tạo ngăn xếp có các phần tử như sau:

Sau đó sử dụng các hàm push(), pop() để hàng đợi có kết quả là:

Để tính giá trị một biểu thức số học bằng máy tính, một số nhà khoa học đã sử dụng cách biểu diễn dạng tiền tố (hay còn gọi là kí pháp Ba lan). Ví dụ, biểu thức số học (2-7/3)*(4-1) sẽ được chuyển sang dạng tiền tố có dạng *-2/73-41 (toán tử đặt trước toán hạng) trước khi tính giá trị. Sử dụng các hàm initStack(), push() để tạo ngăn xếp có các phần tử như sau:

Bước 1: Khởi tạo ngăn xếp và đẩy các phần tử của biểu thức gốc vào ngăn xếp.

Bước 2: Sử dụng ngăn xếp để chuyển đổi biểu thức từ dạng trung tố sang tiền tố bằng cách sử dụng các thao tác push và pop.

Code:

class Stack:

    def __init__(self):

       self.stack = []

    def push(self, item):

       self.stack.append(item)

    def pop(self):

        if not self.is_empty():

           return self.stack.pop()

        return None

    def peek(self):

        if not self.is_empty():

           return self.stack[-1]

        return None

    def is_empty(self):

        return len(self.stack) == 0

def initStack():

    s = Stack()

    elements = ["(", "2", "-", "7", "/", "3", ")", "*", "(", "4", "-", "1", ")"]

    for element in elements:

       s.push(element)

    return s

def infix_to_prefix(stack):

    operators = set(['+', '-', '*', '/', '(', ')'])

    precedence = {'+': 1, '-': 1, '*': 2, '/': 2}

    output = []

   operator_stack = Stack()

    while not stack.is_empty():

        token = stack.pop()

        if token.isdigit():

           output.append(token)

        elif token == '(':

           while not operator_stack.is_empty() and operator_stack.peek() != ')':

               output.append(operator_stack.pop())

           operator_stack.pop()  # pop ')'

        elif token == ')':

           operator_stack.push(token)

        else:

           while (not operator_stack.is_empty() and 

                  precedence.get(token, 0) <= precedence.get(operator_stack.peek(), 0)):

               output.append(operator_stack.pop())

           operator_stack.push(token)

    while not operator_stack.is_empty():

       output.append(operator_stack.pop())

    return output[::-1]  # Đảo ngược danh sách để có dạng tiền tố

# Khởi tạo ngăn xếp

stack = initStack()

# Chuyển biểu thức từ trung tố sang tiền tố

result = infix_to_prefix(stack)

# In kết quả

print(" ".join(result))  # Output: * - 2 / 7 3 - 4 1

Giải thích:

- Lớp Stack: Định nghĩa các phương thức cơ bản cho ngăn xếp (push, pop, peek, is_empty).

- Hàm initStack(): Khởi tạo ngăn xếp và đẩy các phần tử của biểu thức vào ngăn xếp.

- Hàm infix_to_prefix(): Chuyển đổi biểu thức từ dạng trung tố sang tiền tố bằng cách sử dụng ngăn xếp. Hàm này đọc từng phần tử từ ngăn xếp, xử lý các toán tử và toán hạng theo nguyên tắc của biểu thức tiền tố, và đẩy kết quả cuối cùng vào danh sách output.

- Kết quả: In ra biểu thức tiền tố.