Chuyên đề Tin 12 CTST Bài 2.3. Cây tìm kiếm nhị phân

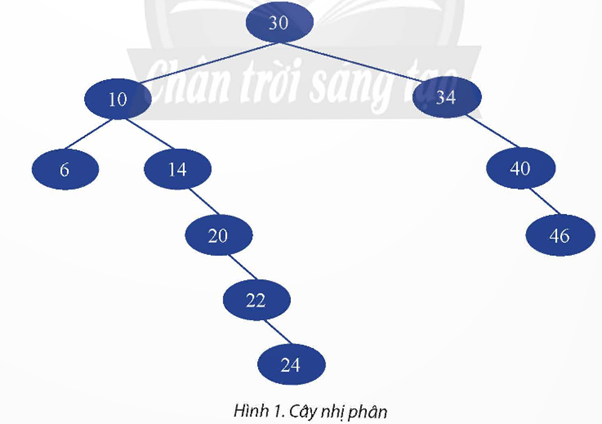
Để tìm kiếm giá trị x = 20 trong tập hợp A, ta có thể làm như sau:

a)  Bắt đầu từ phần tử đầu tiên của mảng A, so sánh từng phần tử với x. Khi bạn đến phần tử thứ tám, bạn sẽ thấy giá trị 20. Đó là tìm kiếm tuần tự.

b) Tìm kiếm x trong cây nhị phân: Giả sử tập hợp A được tổ chức thành một cây tìm kiếm nhị phân, bạn sẽ bắt đầu từ nút gốc và so sánh x với giá trị của nút. Nếu x nhỏ hơn, di chuyển sang nút con bên trái; nếu lớn hơn, di chuyển sang nút con bên phải. Tiếp tục quá trình này cho đến khi tìm thấy x hoặc đến nút lá mà không tìm thấy x. Con đường cụ thể phụ thuộc vào cách tập hợp A được sắp xếp trong cây.

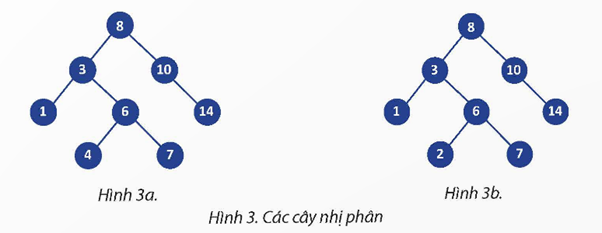
 “Hình 3b” biểu diễn cây tìm kiếm nhị phân. Vì mỗi nút đều tuân theo quy tắc: tất cả các phần tử ở cây con bên trái đều nhỏ hơn giá trị của nút gốc, và tất cả các phần tử ở cây con bên phải đều lớn hơn giá trị của nút gốc.

Ví dụ, dưới nút gốc ‘8’, tất cả các giá trị trong cây con bên trái (‘1’, ‘2’, ‘3’, ‘6’, và ‘7’) đều nhỏ hơn ‘8’, trong khi tất cả các giá trị trong cây con bên phải (‘10’, và ‘14’) đều lớn hơn ‘8’.

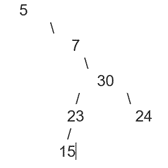
Để vẽ cây tìm kiếm nhị phân (Binary Search Tree - BST) từ mảng A = [5, 7, 30, 23, 34, 15], ta cần lần lượt chèn từng phần tử của mảng vào cây theo quy tắc của cây tìm kiếm nhị phân:

1.    Nếu cây rỗng, phần tử đầu tiên sẽ là gốc.

2.    Với mỗi phần tử tiếp theo:

Nếu phần tử nhỏ hơn hoặc bằng nút hiện tại, chèn vào cây con bên trái.

Nếu phần tử lớn hơn nút hiện tại, chèn vào cây con bên phải.

Bắt đầu từ mảng A = [5, 7, 30, 23, 34, 15]:

1. Phần tử đầu tiên là 5, nó sẽ là gốc.

2. Chèn 7 vào cây:

7      > 5, nên 7 là con phải của 5.

3. Chèn 30 vào cây:

30 > 5, chuyển sang cây con phải của 5.

30    7, nên 30 là con phải của 7.

4. Chèn 23 vào cây:

23 > 5, chuyển sang cây con phải của 5.

23 > 7, chuyển sang cây con phải của 7.

23    30, nên 23 là con trái của 30.

5. Chèn 34 vào cây:

34 > 5, chuyển sang cây con phải của 5.

34 > 7, chuyển sang cây con phải của 7.

34    30, nên 34 là con phải của 30.

6. Chèn 15 vào cây:

15 > 5, chuyển sang cây con phải của 5.

15 > 7, chuyển sang cây con phải của 7.

15 < 30, chuyển sang cây con trái của 30.

15 < 23, nên 15 là con trái của 23.

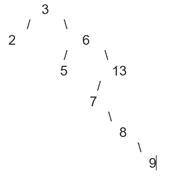
Vẽ cây tìm kiếm nhị phân bằng cách đưa vào cây rỗng lần lượt các phần tử của mảng A = [3, 6, 13, 7, 5, 2, 8, 9] như sau:

1. Phần tử đầu tiên là 3, nó sẽ là gốc.

2. Chèn các phần tử còn lại lần lượt vào cây theo quy tắc của cây tìm kiếm nhị phân.

Bắt đầu từ mảng A = [3, 6, 13, 7, 5, 2, 8, 9]:

1. Phần tử đầu tiên là 3, nó sẽ là gốc.

markdown

Sao chép mã 3

1. Chèn 6 vào cây: 6 > 3, nên 6 là con phải của 3.

2. Chèn 13 vào cây: 13 > 3, chuyển sang cây con phải của 3. 13 > 6, nên 13 là con phải của 6.

3. Chèn 7 vào cây: 7 > 3, chuyển sang cây con phải của 3. 7 > 6, chuyển sang cây con phải của 6. 7 < 13, nên 7 là con trái của 13.

4. Chèn 5 vào cây: 5 > 3, chuyển sang cây con phải của 3. 5 < 6, nên 5 là con trái của 6.

5. Chèn 2 vào cây: 2 < 3, nên 2 là con trái của 3.

6. Chèn 8 vào cây:

8 > 3, chuyển sang cây con phải của 3.

8 > 6, chuyển sang cây con phải của 6.

8 < 13, chuyển sang cây con trái của 13.

8 > 7, nên 8 là con phải của 7.

    Chèn 9 vào cây:

9 > 3, chuyển sang cây con phải của 3.

9 > 6, chuyển sang cây con phải của 6.

9 < 13, chuyển sang cây con trái của 13.

9 > 7, chuyển sang cây con phải của 7.

9 > 8, nên 9 là con phải của 8.

Thuật toán để xác định giá trị * = 34 có thuộc cây tìm kiếm nhị phân được biểu diễn ở Hình 4b hay không được thực hiện bằng cách duyệt cây từ gốc xuống đến khi tìm thấy giá trị hoặc đến khi không còn nút nào để duyệt.

Thuật toán như sau:

Cách 1: Sử dụng các phép toán duyệt trước, duyệt giữa, duyệt sau để xác định giá trị x = 34 có thuộc cây tìm kiếm nhị phần ở Hình 4 hay không.

Ví dụ: Sử dụng phép duyệt trước để tìm giá trị x

def insertTree(T, i, v):

if 1 >= len(T):

T.extend([None]*(i-len(T)+1))

if T[i]== None:

T[i]= v== quân thi sáng ngà

print("Đã tồn tại nút có giá trị bằng", v)

elif v<T[i]:

insertTree(T, 2*1+ 1, v)

else:

insertTree(T, 2*i +2, v)

def createBSTTree(T, a):

for v in a:

insertTree (T, 0, v)

def preorderSearch (T, i, x):

global found

if i < len(T) and T[1] != None: if T[i] == x:

found = True

return

else:

preorderSearch(T, 2*i + 1, x)

preorderSearch(T, 2*1 + 2, x)

def Search(T, x):

global found

found = False

preorderSearch(T, 0, x) return found

a =list(map (int, input().split()))

x = int(input())

T = []

createBSTTree(T, a)

found Search(T, x)

print (found)

Cách 2: Sử dụng thuật toán đệ quy search(T, i, x) để tìm kiếm x trên cây tìm kiếm nhị phân T gốc i.

Mã nguồn hàm tìm kiếm giá trị trên cây tìm kiếm nhị phân sử dụng đệ quy:

Em có thể sử dụng đệ quy hoặc vòng lặp để tìm một nút trên cây tìm kiếm nhị phần. Hàm đệ quy search(T, i, x) dùng để tìm kiếm giá trị x trên cây tim kiếm nhị phần T gốc i.

#Tìm x trên cây tìm kiếm nhị phân T gốc 1

def search(T, i, x):

if i >= len(T) or T[i] == None:

return False

X:

#Cây T gốc i là rỗng #không tìm thấy x

#Tìm thấy x

elif T[i]

return True

elif x <T[i]:

else:

return search(T, 2*1+2, x)

#Tim x trên cây con phải

return search(T, 2*1+1, x)

#Tim x trên cây con trái