Chuyên đề Tin 12 CTST Bài 2.4. Thực hành cây tìm kiếm nhị phân

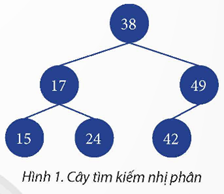
Để xuất giá trị các nút của cây tìm kiếm nhị phân trong Hình 1 theo thứ tự tăng dần, bạn có thể sử dụng thuật toán duyệt giữa (in-order traversal). Thuật toán này sẽ duyệt qua các nút theo trình tự: nút con bên trái, nút gốc, và nút con bên phải. Dưới đây là các bước cụ thể:

Bắt đầu từ nút gốc (38), di chuyển xuống nút con bên trái (17).

Từ nút 17, tiếp tục di chuyển xuống nút con bên trái nhất (15), đây là nút không có con bên trái nên in giá trị 15.

Quay trở lại nút 17 và in giá trị 17.

Di chuyển đến nút con bên phải của nút 17 (24) và in giá trị 24.

Quay trở lại nút gốc 38 và in giá trị 38.

Di chuyển đến nút con bên phải của nút gốc (49), rồi di chuyển xuống nút con bên trái của nó (42) và in giá trị 42.

Cuối cùng, in giá trị của nút 49.

Kết quả của thuật toán duyệt giữa sẽ là dãy số theo thứ tự tăng dần: 15, 17, 24, 38, 42, 49. Đây là cách mà các giá trị nút được xuất ra một cách có trật tự từ cây tìm kiếm nhị phân.

Sử dụng chương trình tạo cây tìm kiếm nhị phân và chương trình con tìm kiếm

ở Bài 2.3 để thực hiện yêu cầu trên.

Mã nguồn tham khảo:

#Tìm x trên cây tìm kiếm nhị phân T gốc i

def search(T, i, x):

if i = len(T) or T[i] == None:

return False

elif T[i]== X:

return True

elif x <T[i]:

#Cây T gốc i là rỗng

“Không tìm thấy x

#Tìm thấy x

else:

return search (T, 2*1+1, x)

return search(T, 2*1+2, x)

#Tìm x trên cây con trái

#Tìm x trên cây con phải

#Thêm giá trị v vào cây tìm kiếm nhị phân T gốc i def insertTree(T, i, v):

if i>=len(T):

T.extend([None]*(i-len(T)+1))

if T[i]

== None:

T[i] = V

elif v == T[i]:

print("Đã tồn tại nút có giá trị bằng", v)

elif v<T[i]:

else:

insertTree(T, 2*i + 1, v)

insertTree(T, 2*i + 2, v)

#Tạo cây tìm kiếm nhị phân T từ mảng a def createBSTTree(T, a): for i in range(len(a)):

insertTree(T, 0, a[i])

def printTree(T):

for i in T:

if i!=None:

print(1, end=" ")

def inOrderTraversal (tree, i):

if i < len(tree) and tree[i] != None: inOrderTraversal (tree, 2*i + 1) print(tree[i], end = ')

inOrderTraversal (tree, 2*i + 2)

print("nhập danh sách các số để tạo cây: ")

a = list(map(int, input().split())) print("nhập giá trị cần tìm: ") x= int(input())

T = []

#Thêm a[i] vào cây T

#Cây gốc i khác rỗng #Duyệt cây con trái HXử lí nút gốc #Duyệt cây con phải

createBSTTree (T,a)

A printTree(T) 43. print()

print (search (T, 0,

để trời sáng tạo

inOrderTraversal (T,0)

Thực hiện các bước sau:

Tạo cây tìm kiếm nhị phân T tử mảng an

Duyệt giữa cây tìm kiếm nhị phân T.

Code như sau:

def insertTreeT(T, i, v):

if i len(T):

T.extend([None]*(i-len(T)+1))

if T[i]== None:

T[i] = v

elif v<T[i]:

else:

insertTreeT(T, 2*i + 1, v)

insertTreeT(T, 2*i + 2, v)

def createBSTTree (T, a):

for i in range(len(a)):

insertTreeT(T, 0, a[i])

def inOrderSort (T, i, a):

if i < len(T) and T[i] != None: inOrderSort (T, 2*i + 1, a) a.append(T[i])

inOrderSort (T, 2*i + 2, a)

def SortBST(a):

T = []

createBSTTree (T, a)

a.clear()

inOrderSort (T, 0, a)

print("Nhập mảng cần sắp xếp tăng dần: ") a = list(map(int, input().split())) SortBST(a)

print("Mảng có thứ tự tăng dần:", a)

Chương trình để giúp bác thợ mộc tìm thanh gỗ đúng với kích thước đã cho.

Code như sau:

def find_wood_plank(wood_lengths, k):

    Hàm này tìm kiếm thanh gỗ có kích thước k trong danh sách wood_lengths.

    Parameters:

    wood_lengths (list): Danh sách kích thước các thanh gỗ.

    k (int): Kích thước của thanh gỗ cần tìm.

    Returns:

    bool: True nếu tìm thấy thanh gỗ có kích thước k, False nếu không tìm thấy.

    for length in wood_lengths:

        if length == k:

           return True

    return False

# Nhập vào danh sách các kích thước thanh gỗ và kích thước cần tìm

n = int(input("Nhập số lượng thanh gỗ: "))

wood_lengths = []

print("Nhập kích thước của từng thanh gỗ:")

for _ in range(n):

   wood_lengths.append(int(input()))

k = int(input("Nhập kích thước thanh gỗ cần tìm: "))

# Kiểm tra xem có thanh gỗ có kích thước k hay không

if find_wood_plank(wood_lengths, k):

   print(f"Tìm thấy thanh gỗ có kích thước {k} cm.")

else:

   print(f"Không tìm thấy thanh gỗ có kích thước {k} cm.")

a) Viết chương trình tạo cây tìm kiếm nhị phân T biểu diễn tập hợp A

Code như sau:

class TreeNode:

    def __init__(self, value):

       self.value = value

       self.left = None

       self.right = None

def insert(root, value):

    if root is None:

        return TreeNode(value)

    else:

        if value < root.value:

           root.left = insert(root.left, value)

        else:

           root.right = insert(root.right, value)

    return root

def build_bst(values):

    root = None

    for value in values:

        root = insert(root, value)

    return root

# Tập hợp số nguyên dương A

A = {28, 21, 43, 13, 23, 35, 50, 10, 15, 22, 27, 30, 40, 47, 52}

# Tạo cây tìm kiếm nhị phân T

root = build_bst(A)

b) Vẽ minh hoạ cây T

Chúng ta sẽ lần lượt chèn các giá trị vào cây BST. Dưới đây là cách cây T sẽ trông như sau khi tất cả các giá trị đã được chèn vào:

javascript

Sao chép mã

c) Viết chương trình kiểm tra giá trị x = 10 có xuất hiện trong cây tìm kiếm nhị phân T hay không

Dưới đây là chương trình kiểm tra giá trị x = 10 có xuất hiện trong cây tìm kiếm nhị phân T hay không:

def search_bst(node, value):

    if node is None:

        return False

    if node.value == value:

        return True

    elif value < node.value:

        return search_bst(node.left, value)

    else:

        return search_bst(node.right, value)

# Kiểm tra giá trị x = 10

x = 10

if search_bst(root, x):

   print(f"Giá trị {x} có trong cây.")

else:

   print(f"Giá trị {x} không có trong cây.")

d) Viết chương trình xuất ra màn hình các giá trị của tập hợp A được sắp xếp giảm dần

Dưới đây là chương trình để xuất ra màn hình các giá trị của tập hợp A được sắp xếp giảm dần:

def inorder_traversal(node, result):

    if node is not None:

       inorder_traversal(node.left, result)

       result.append(node.value)

       inorder_traversal(node.right, result)

def sorted_descending_bst(root):

    result = []

   inorder_traversal(root, result)

    return sorted(result, reverse=True)

# Xuất ra màn hình các giá trị của tập hợp A được sắp xếp giảm dần

sorted_values = sorted_descending_bst(root)

print("Các giá trị của tập hợp A được sắp xếp giảm dần:")

print(sorted_values)

Tổng hợp chương trình

Dưới đây là chương trình đầy đủ bao gồm tất cả các phần:

class TreeNode:

    def __init__(self, value):

       self.value = value

       self.left = None

       self.right = None

def insert(root, value):

    if root is None:

        return TreeNode(value)

    else:

        if value < root.value:

           root.left = insert(root.left, value)

        else:

           root.right = insert(root.right, value)

    return root

def build_bst(values):

    root = None

    for value in values:

        root = insert(root, value)

    return root

def search_bst(node, value):

    if node is None:

        return False

    if node.value == value:

        return True

    elif value < node.value:

        return search_bst(node.left, value)

    else:

        return search_bst(node.right, value)

def inorder_traversal(node, result):

    if node is not None:

       inorder_traversal(node.left, result)

       result.append(node.value)

       inorder_traversal(node.right, result)

def sorted_descending_bst(root):

    result = []

   inorder_traversal(root, result)

    return sorted(result, reverse=True)

# Tập hợp số nguyên dương A

A = {28, 21, 43, 13, 23, 35, 50, 10, 15, 22, 27, 30, 40, 47, 52}

# Tạo cây tìm kiếm nhị phân T

root = build_bst(A)

# Kiểm tra giá trị x = 10

x = 10

if search_bst(root, x):

   print(f"Giá trị {x} có trong cây.")

else:

   print(f"Giá trị {x} không có trong cây.")

# Xuất ra màn hình các giá trị của tập hợp A được sắp xếp giảm dần

sorted_values = sorted_descending_bst(root)

print("Các giá trị của tập hợp A được sắp xếp giảm dần:")

print(sorted_values)

Chương trình trên thực hiện các nhiệm vụ yêu cầu từ việc tạo cây tìm kiếm nhị phân, kiểm tra giá trị x = 10, đến việc sắp xếp và xuất ra màn hình các giá trị của tập hợp A theo thứ tự giảm dần.