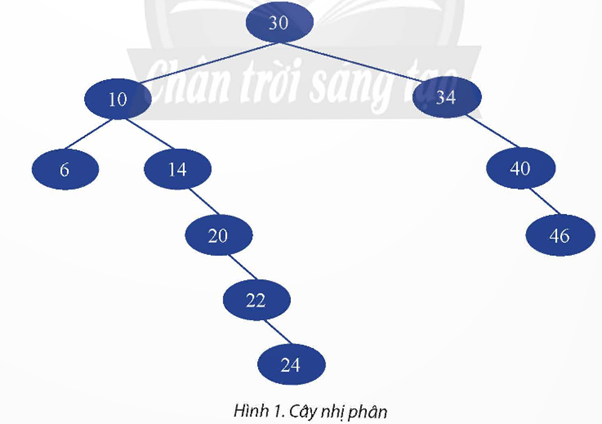
Trình bày thuật toán xác định giá trị * = 34 có thuộc cây tìm kiếm nhị phân được biểu diễn ở Hình 4b hay không.
Trình bày thuật toán xác định giá trị * = 34 có thuộc cây tìm kiếm nhị phân được biểu diễn ở Hình 4b hay không.
Câu hỏi trong đề: Chuyên đề Tin 12 CTST Bài 2.3. Cây tìm kiếm nhị phân !!
Quảng cáo
Trả lời:
Thuật toán để xác định giá trị * = 34 có thuộc cây tìm kiếm nhị phân được biểu diễn ở Hình 4b hay không được thực hiện bằng cách duyệt cây từ gốc xuống đến khi tìm thấy giá trị hoặc đến khi không còn nút nào để duyệt.
Thuật toán như sau:
Cách 1: Sử dụng các phép toán duyệt trước, duyệt giữa, duyệt sau để xác định giá trị x = 34 có thuộc cây tìm kiếm nhị phần ở Hình 4 hay không.
Ví dụ: Sử dụng phép duyệt trước để tìm giá trị x
def insertTree(T, i, v):
if 1 >= len(T):
T.extend([None]*(i-len(T)+1))
if T[i]== None:
T[i]= v== quân thi sáng ngà
print("Đã tồn tại nút có giá trị bằng", v)
elif v<T[i]:
insertTree(T, 2*1+ 1, v)
else:
insertTree(T, 2*i +2, v)
def createBSTTree(T, a):
for v in a:
insertTree (T, 0, v)
def preorderSearch (T, i, x):
global found
if i < len(T) and T[1] != None: if T[i] == x:
found = True
return
else:
preorderSearch(T, 2*i + 1, x)
preorderSearch(T, 2*1 + 2, x)
def Search(T, x):
global found
found = False
preorderSearch(T, 0, x) return found
a =list(map (int, input().split()))
x = int(input())
T = []
createBSTTree(T, a)
found Search(T, x)
print (found)
Cách 2: Sử dụng thuật toán đệ quy search(T, i, x) để tìm kiếm x trên cây tìm kiếm nhị phân T gốc i.
Mã nguồn hàm tìm kiếm giá trị trên cây tìm kiếm nhị phân sử dụng đệ quy:
Em có thể sử dụng đệ quy hoặc vòng lặp để tìm một nút trên cây tìm kiếm nhị phần. Hàm đệ quy search(T, i, x) dùng để tìm kiếm giá trị x trên cây tim kiếm nhị phần T gốc i.
#Tìm x trên cây tìm kiếm nhị phân T gốc 1
def search(T, i, x):
if i >= len(T) or T[i] == None:
return False
X:
#Cây T gốc i là rỗng #không tìm thấy x
#Tìm thấy x
elif T[i]
return True
elif x <T[i]:
else:
return search(T, 2*1+2, x)
#Tim x trên cây con phải
return search(T, 2*1+1, x)
#Tim x trên cây con trái
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay dẫn chứng nghị luận xã hội năm 2025 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Để tìm giá trị x = 22 trong cây tìm kiếm nhị phân, bạn có thể thực hiện theo các bước sau:
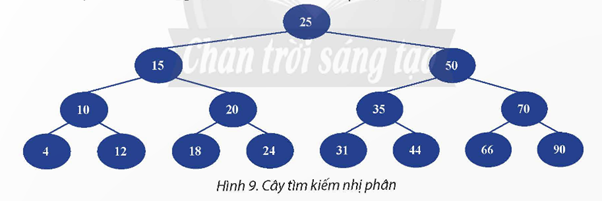
- Duyệt trước: Bắt đầu từ nút gốc (25), duyệt qua nút gốc, sau đó là cây con bên trái (bắt đầu từ 15), và cuối cùng là cây con bên phải (bắt đầu từ 50). Tiếp tục cho đến khi tìm thấy x = 22 hoặc đã duyệt qua tất cả các nút.
- Duyệt giữa: Duyệt cây con bên trái (bắt đầu từ 15), sau đó là nút gốc (25), và cuối cùng là cây con bên phải (bắt đầu từ 50). Phương pháp này sẽ tìm thấy x = 22 sau khi kiểm tra tất cả các giá trị nhỏ hơn.
- Duyệt sau: Duyệt cây con bên trái (bắt đầu từ 15), sau đó là cây con bên phải (bắt đầu từ 50), và cuối cùng là nút gốc (25). Phương pháp này sẽ tìm thấy x = 22 sau khi khám phá tất cả các nút con.
- Tìm kiếm nhị phân: Bắt đầu từ nút gốc (25). Vì x = 22 nhỏ hơn 25, chuyển sang nút con bên trái (15). Vì x = 22 lớn hơn 15, chuyển sang nút con bên phải (20). Vì không có nút con bên phải cho nút có giá trị ‘20’, kết luận rằng x = 22 không tồn tại trong cây tìm kiếm nhị phân này.
b) Trong trường hợp tổng quát của cây tìm kiếm nhị phân, thuật toán tìm kiếm nhị phân thường có số lần so sánh ít nhất vì nó hệ thống hóa việc thu hẹp vị trí có thể có bằng cách so sánh ở mỗi cấp độ.
c) Chương trình tạo cây tìm kiếm nhị phân ở Hình 9. Sau đó, in ra màn hình các khóa có trong cây này theo thứ tự tăng dần.ưới đây là mã chương trình để tạo cây tìm kiếm nhị phân như trong Hình 9 và in ra các khóa theo thứ tự tăng dần:
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
def insert(root, key):
if root is None:
return Node(key)
else:
if root.val < key:
root.right = insert(root.right, key)
else:
root.left = insert(root.left, key)
return root
def inorder_traversal(root):
if root:
inorder_traversal(root.left)
print(root.val, end=' ')
inorder_traversal(root.right)
# Tạo cây tìm kiếm nhị phân từ các giá trị trong Hình 9
values = [25, 15, 50, 10, 20, 35, 70, 12, 18, 24, 31, 44, 66, 90]
root = Node(values[0])
for value in values[1:]:
insert(root, value)
# In các khóa theo thứ tự tăng dần
inorder_traversal(root)
Lời giải
Vẽ cây tìm kiếm nhị phân bằng cách đưa vào cây rỗng lần lượt các phần tử của mảng A = [3, 6, 13, 7, 5, 2, 8, 9] như sau:
1. Phần tử đầu tiên là 3, nó sẽ là gốc.
2. Chèn các phần tử còn lại lần lượt vào cây theo quy tắc của cây tìm kiếm nhị phân.
Bắt đầu từ mảng A = [3, 6, 13, 7, 5, 2, 8, 9]:
1. Phần tử đầu tiên là 3, nó sẽ là gốc.
markdown
Sao chép mã 3
1. Chèn 6 vào cây: 6 > 3, nên 6 là con phải của 3.
2. Chèn 13 vào cây: 13 > 3, chuyển sang cây con phải của 3. 13 > 6, nên 13 là con phải của 6.
3. Chèn 7 vào cây: 7 > 3, chuyển sang cây con phải của 3. 7 > 6, chuyển sang cây con phải của 6. 7 < 13, nên 7 là con trái của 13.
4. Chèn 5 vào cây: 5 > 3, chuyển sang cây con phải của 3. 5 < 6, nên 5 là con trái của 6.
5. Chèn 2 vào cây: 2 < 3, nên 2 là con trái của 3.
6. Chèn 8 vào cây:
8 > 3, chuyển sang cây con phải của 3.
8 > 6, chuyển sang cây con phải của 6.
8 < 13, chuyển sang cây con trái của 13.
8 > 7, nên 8 là con phải của 7.
Chèn 9 vào cây:
9 > 3, chuyển sang cây con phải của 3.
9 > 6, chuyển sang cây con phải của 6.
9 < 13, chuyển sang cây con trái của 13.
9 > 7, chuyển sang cây con phải của 7.
9 > 8, nên 9 là con phải của 8.
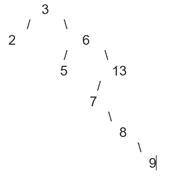
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.