Câu hỏi:
02/10/2024 1,243
Giải bất phương trình ẩn \[x\] sau: \[\frac{{x - ab}}{{a + b}} + \frac{{x - bc}}{{b + c}} + \frac{{x - ac}}{{a + c}} > a + b + c\] với \[a,\,\,b,\,\,c > 0\].
Giải bất phương trình ẩn \[x\] sau: \[\frac{{x - ab}}{{a + b}} + \frac{{x - bc}}{{b + c}} + \frac{{x - ac}}{{a + c}} > a + b + c\] với \[a,\,\,b,\,\,c > 0\].
Câu hỏi trong đề:
Đề thi giữa kì 1 môn Toán lớp 9 Cánh diều có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giải bất phương trình:
\[\frac{{x - ab}}{{a + b}} + \frac{{x - bc}}{{b + c}} + \frac{{x - ac}}{{a + c}} > a + b + c\]
\[\frac{{x - ab}}{{a + b}} + \frac{{x - bc}}{{b + c}} + \frac{{x - ac}}{{a + c}} - a - b - c > 0\]
\[\left( {\frac{{x - ab}}{{a + b}} - c} \right) + \left( {\frac{{x - bc}}{{b + c}} - a} \right) + \left( {\frac{{x - ac}}{{a + c}} - b} \right) > 0\]
\[\left( {\frac{{x - ab - ac - bc}}{{a + b}}} \right) + \left( {\frac{{x - bc - ab - ac}}{{b + c}}} \right) + \left( {\frac{{x - ac - ab - bc}}{{a + c}}} \right) > 0\]
\[\left( {x - ab - ac - bc} \right)\left( {\frac{1}{{a + b}} + \frac{1}{{b + c}} + \frac{1}{{a + c}}} \right) > 0\] (*)
Nhận thấy \[\frac{1}{{a + b}} + \frac{1}{{b + c}} + \frac{1}{{a + c}} > 0\] với \[a,\,\,b,\,\,c > 0\].
Do đó, từ (*) ta suy ra \[x - ab - ac - bc > 0\] suy ra \[x > ab + bc + ac\]\[\left( {a,\,\,b,\,\,c > 0} \right)\].
Vậy nghiệm của bất phương trình đã cho là \[x > ab + bc + ac\] với \[\left( {a,\,\,b,\,\,c > 0} \right)\].
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
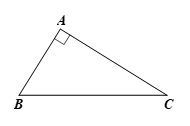
Cho tam giác \(ABC\) vuông tại \(A\). Khi đó, \(\sin \widehat {ABC}\) bằng:
Xem đáp án »
02/10/2024
1,909
Câu 2:
Điều kiện xác định của phương trình \(\frac{1}{{x\left( {{x^2} + 4} \right)}} = \frac{{x + 1}}{x} - \frac{1}{{x - 2}}\) là
Xem đáp án »
02/10/2024
1,312
Câu 3:
Từ một đài quan sát, một người đặt mắt tại vị trí \[B.\] Người đó nhìn thấy một chiếc ô tô ở vị trí \[C\] theo phương \[BC\] tạo với phương nằm ngang \[Bx\] một góc là \(\widehat {CBx} = 25^\circ \) với \[Bx\,{\rm{//}}\,AC.\] Khi đó, khoảng cách giữa ô tô và chân đài quan sát là \[AC = 1,221{\rm{\;km}}{\rm{.}}\] Nếu ô tô từ vị trí \[C\] tiếp tục đi về phía chân đài quan sát với tốc độ \[60\] km/h thì sau 1 phút, người đó nhìn thấy ô tô ở vị trí \[D\] với góc \(\widehat {DBx} = \alpha \) (hình vẽ).
a) Tính chiều cao của đài quan sát (làm tròn kết quả đến hàng đơn vị của mét), biết độ cao từ tầm mắt của người đó đến đỉnh đài quan sát là \[3\] m.
b) Tính số đo góc \[\alpha \] (làm tròn kết quả đến hàng đơn vị của phút).
c) Tính khoảng cách từ mắt người quan sát đến vị trí \[D\] (làm tròn kết quả đến hàng đơn vị của mét).
Xem đáp án »
02/10/2024
754
Câu 4:
Cho \(\alpha \) và \(\beta \) là hai góc nhọn bất kì thỏa mãn \(\alpha + \beta = 90^\circ .\) Khẳng định nào sau đây là đúng?
Xem đáp án »
02/10/2024
711
Câu 5:
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
Xem đáp án »
02/10/2024
642
Câu 6:
Cho tam giác \(MNP\) vuông tại \(M\) có \(MP = 4\) và \(\widehat {P\,} = 30^o .\) Nhận định nào sau đây là sai?
Xem đáp án »
02/10/2024
459
Bình luận
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
23 câu Trắc nghiệm Toán 9 Bài 1: Căn thức bậc hai có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 02
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 03
-
21 câu Trắc nghiệm Toán 9 Bài 1: Căn bậc hai có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 04
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 06
về câu hỏi!