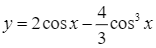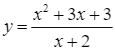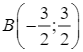Cho tứ diện \(ABCD\) và điểm \(G\) thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \) (\(G\) là trọng tâm của tứ diện). Gọi \({G_0}\) là giao điểm của \(GA\) và mặt phẳng \(\left( {BCD} \right)\). Trong các khẳng định sau, khẳng định nào đúng?
Cho tứ diện \(ABCD\) và điểm \(G\) thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \) (\(G\) là trọng tâm của tứ diện). Gọi \({G_0}\) là giao điểm của \(GA\) và mặt phẳng \(\left( {BCD} \right)\). Trong các khẳng định sau, khẳng định nào đúng?
D. \(\overrightarrow {GA} = 2\overrightarrow {{G_0}G} \).
Quảng cáo
Trả lời:
Đáp án đúng là: C
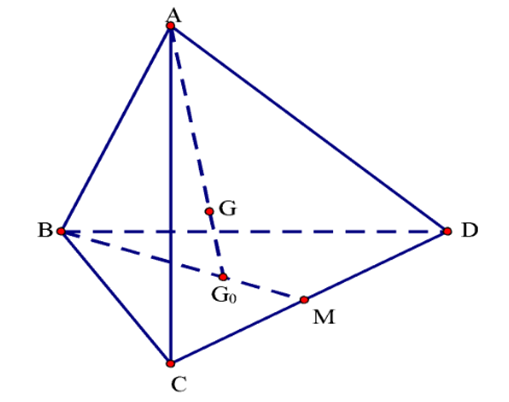
Vì \({G_0}\) là giao điểm của \(GA\) và mặt phẳng \(\left( {BCD} \right)\) nên ta suy ra được \({G_0}\) là trọng tâm của tam giác \(BCD\). Do đó, \(\overrightarrow {{G_0}B} + \overrightarrow {{G_0}C} + \overrightarrow {{G_0}D} = \overrightarrow 0 \).
Ta có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
Suy ra \(\overrightarrow {GA} = - \left( {\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = - \left( {3\overrightarrow {G{G_0}} + \overrightarrow {{G_0}B} + \overrightarrow {{G_0}C} + \overrightarrow {{G_0}D} } \right) = - 3\overrightarrow {G{G_0}} = 3\overrightarrow {{G_0}G} \).
Vậy \(\overrightarrow {GA} = 3\overrightarrow {{G_0}G} \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có vận tốc tức thời là: ![]() .
.
Xét hàm số ![]() với
với ![]() .
.
Ta có ![]() . Trên khoảng
. Trên khoảng ![]() ,
, ![]() .
.
![]() .
.
Suy ra ![]() .
.
Vậy vận tốc tức thời đạt giá trị lớn nhất bằng ![]() m/s.
m/s.
Đáp số: ![]() .
.
Lời giải
Đáp án đúng là: C
Đặt ![]() . Vì
. Vì ![]() nên
nên ![]() .
.
Khi đó, ta có hàm số 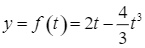 . Ta có
. Ta có ![]() .
.
Trên khoảng ![]() ,
, 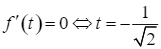 hoặc
hoặc 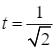 .
.
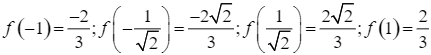 .
.
Suy ra 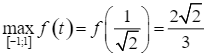 . Vậy
. Vậy 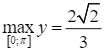 .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng ![]() và
và ![]() .
.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
D. Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng ![]() và
và ![]() .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.