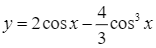Cho hàm số 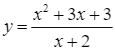 .
.
a) Hàm số đã cho đồng biến trên 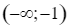 và
và 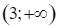 .
.
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng 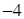 .
.
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm 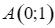 .
.
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng 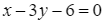 đi qua điểm
đi qua điểm 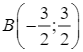 .
.
Cho hàm số 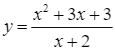 .
.
a) Hàm số đã cho đồng biến trên ![]() và
và ![]() .
.
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng ![]() .
.
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm ![]() .
.
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng ![]() đi qua điểm
đi qua điểm 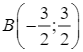 .
.
Quảng cáo
Trả lời:
a) S, b) S, c) Đ, d) Đ.
Xét hàm số 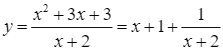 .
.
– Tập xác định của hàm số là ![]() .
.
– Ta có 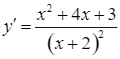 ;
; ![]() khi
khi ![]() hoặc
hoặc ![]() .
.
Bảng biến thiên của hàm số như sau:
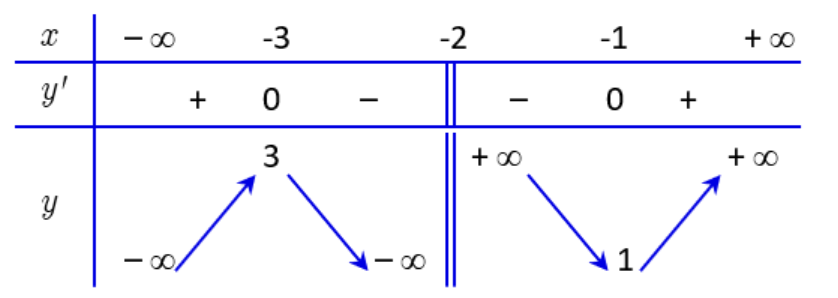
– Hàm số đã cho đồng biến trên từng khoảng ![]() và
và ![]() . Do đó, ý a) sai.
. Do đó, ý a) sai.
– Hàm số đã cho đạt cực đại tại ![]() ,
, ![]() ; đạt cực tiểu tại
; đạt cực tiểu tại ![]() ,
, ![]() .
.
Suy ra ![]() . Do đó, ý b) sai.
. Do đó, ý b) sai.
– Tiệm cận:
+) Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng ![]() .
.
+) Tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng ![]() .
.
Với ![]() thì
thì ![]() , do đó đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm
, do đó đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm ![]() . Vậy ý c) đúng.
. Vậy ý c) đúng.
– Đường thẳng ![]()
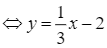 có hệ số góc
có hệ số góc 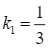 . Đường thẳng này vuông góc với tiếp tuyến của đồ thị hàm số đã cho nên tiếp tuyến này có hệ số góc
. Đường thẳng này vuông góc với tiếp tuyến của đồ thị hàm số đã cho nên tiếp tuyến này có hệ số góc 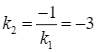 .
.
Khi đó, với ![]() là hoành độ của tiếp điểm thì
là hoành độ của tiếp điểm thì 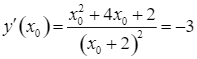 .
.
Ta tìm được 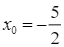 hoặc
hoặc 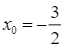 .
.
+) Với 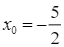 , ta có tiếp tuyến:
, ta có tiếp tuyến: ![]() .
.
+) Với 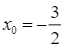 , ta có tiếp tuyến:
, ta có tiếp tuyến: ![]() , tiếp tuyến này đi qua điểm
, tiếp tuyến này đi qua điểm 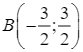 .
.
Do đó, ý d) đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có vận tốc tức thời là: ![]() .
.
Xét hàm số ![]() với
với ![]() .
.
Ta có ![]() . Trên khoảng
. Trên khoảng ![]() ,
, ![]() .
.
![]() .
.
Suy ra ![]() .
.
Vậy vận tốc tức thời đạt giá trị lớn nhất bằng ![]() m/s.
m/s.
Đáp số: ![]() .
.
Lời giải
Đáp án đúng là: C
Đặt ![]() . Vì
. Vì ![]() nên
nên ![]() .
.
Khi đó, ta có hàm số 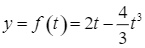 . Ta có
. Ta có ![]() .
.
Trên khoảng ![]() ,
, 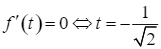 hoặc
hoặc 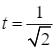 .
.
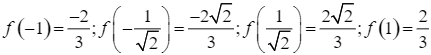 .
.
Suy ra 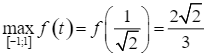 . Vậy
. Vậy 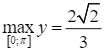 .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng ![]() và
và ![]() .
.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
D. Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng ![]() và
và ![]() .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.