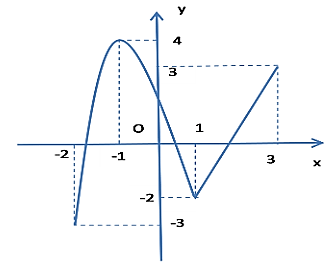
B. Hàm số đạt giá trị nhỏ nhất bằng \(\frac{3}{4}\) và giá trị lớn nhất bằng \(1\).
C. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất.
D. Hàm số đạt giá trị lớn nhất tại điểm có hoành độ \(x = 1\) và giá trị lớn nhất bằng \(1\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 12 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
Tập xác định: \(D = \left[ {1; + \infty } \right)\).
Ta có: \(y' = 1 - \frac{1}{{2\sqrt {x - 1} }} = \frac{{2\sqrt {x - 1} - 1}}{{2\sqrt {x - 1} }}\).
\(y' = 0 \Leftrightarrow \frac{{2\sqrt {x - 1} - 1}}{{2\sqrt {x - 1} }} = 0\)\( \Leftrightarrow 2\sqrt {x - 1} = 1 \Leftrightarrow x = \frac{5}{4}\).
Ta có bảng biến thiên như sau:
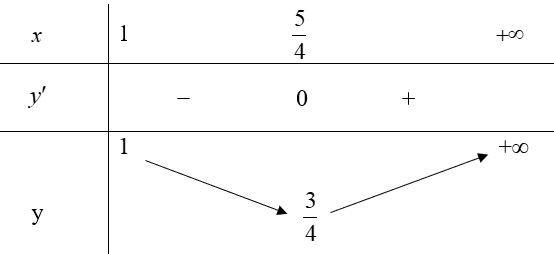
Từ bảng biến thiên ta thấy:
Hàm số có giá trị nhỏ nhất là \(\frac{3}{4}\) và không có giá trị lớn nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét: \(h(t) = - \frac{1}{3}{t^3} + 5{t^2} + 24t\), \(\left( {t > 0} \right).\)
Ta có: \(h'(t) = - {t^2} + 10t + 24\)
\(h'(t) = 0 \Leftrightarrow - {t^2} + 10t + 24 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 12 \in \left( {0; + \infty } \right)\\t = - 2 \notin \left( {0; + \infty } \right)\end{array} \right.\)
Bảng biến thiên:
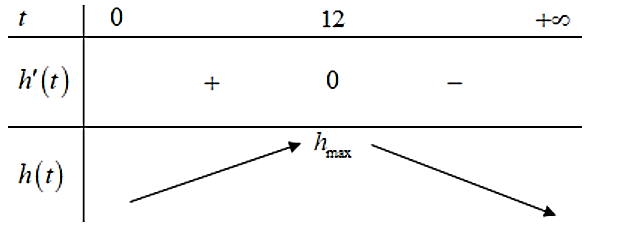
Để mực nước lên cao nhất thì phải mất 12 giờ.
Vậy phải thông báo cho dân dời đi vào 15 giờ chiều cùng ngày.
Câu 2
Lời giải
Đáp án đúng là: A
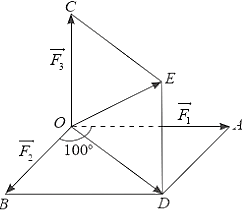
Gọi \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) là ba lực tác động vào vật tại điểm \(O\) lần lượt có độ lớn \(25N,12N,4N\).
Vẽ \(\overrightarrow {OA} = \overrightarrow {{F_1}} ,\overrightarrow {OB} = \overrightarrow {{F_2}} ,\overrightarrow {OC} = \overrightarrow {{F_3}} \).
Dựng hình bình hành \(OADB\) và hình bình hành \(ODEC\).
Hợp lực tác động vào vật là:
\(\overrightarrow F = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {OE} .\)
Áp dụng định lí côsin trong tam giác \(OBD\), ta có:
\(O{D^2} = B{D^2} + O{B^2} - 2.BD.OB.\cos \widehat {OBD} = O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ \)
Vì \(OC \bot \left( {OADB} \right)\) nên \(OC \bot OD\), suy ra \(ODEC\) là hình chữ nhật.
Do đó, tam giác \(DOE\) vuông tại \(D\).
Ta có: \(O{E^2} = O{C^2} + O{D^2} = O{C^2} + O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ \).
Suy ra:
\(OE = \sqrt {O{C^2} + O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ } \)\( = \sqrt {{4^2} + {{25}^2} + {{12}^2} + 2.25.12.\cos 100^\circ } \)
\(OE \approx 26N\).
Vậy độ lớn của hợp lực \(F = OE \approx 26N\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.