Câu hỏi:
13/10/2024 486Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(M\) là trung điểm của \(BC\).
Tính \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right)\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
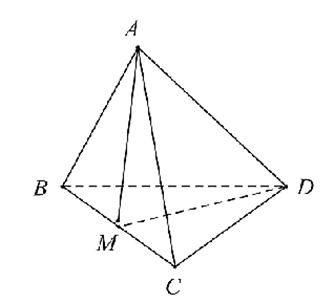
Xét tứ diện
\(ABCD\) cạnh \(a\) ta có: \(\overrightarrow {DM} = \frac{{a\sqrt 3 }}{2};AM = \frac{{a\sqrt 3 }}{2}\).
Ta có: \(\overrightarrow {AB} .\overrightarrow {DM} = \overrightarrow {AB} .\left( {\overrightarrow {AM} - \overrightarrow {AD} } \right) = \overrightarrow {AB} .\overrightarrow {AM} - \overrightarrow {AB} .\overrightarrow {AD} \)
\( = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AM} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AM} } \right) - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right)\)
= \(a.\frac{{a\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} - a.a.\frac{1}{2} = \frac{{{a^2}}}{4}\).
Ta có: \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right)\) = \(\frac{{\overrightarrow {AB} .\overrightarrow {DM} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {DM} } \right|}} = \frac{{\frac{{{a^2}}}{4}}}{{a.\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{6}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: C
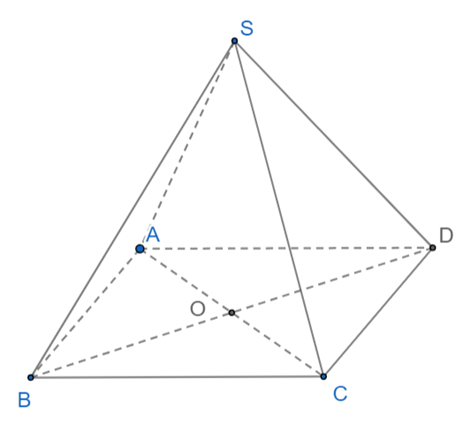
Ta có:
\(\overrightarrow u = \overrightarrow {SA} - \overrightarrow {SC} = \overrightarrow {SA} + \overrightarrow {CS} = \overrightarrow {CA} \).
Suy ra \(\left| {\overrightarrow u } \right| = \left| {\overrightarrow {SA} - \overrightarrow {SC} } \right| = \left| {\overrightarrow {CA} } \right| = \sqrt {{{\left( {2\sqrt 3 } \right)}^2} + {{\left( {2\sqrt 3 } \right)}^2}} = 2\sqrt 6 .\)
Lời giải
Đáp án đúng là: D
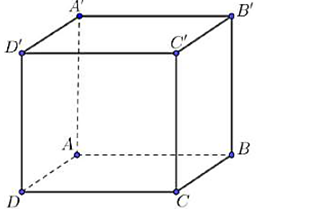
Ta có:
\(ABCD.A'B'C'D'\) là hình lập phương.
Do đó, \(\left( {\overrightarrow {AB} ,\overrightarrow {A'D'} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {DAB} = 90^\circ ;\)
\(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = 45^\circ \);
\(\left( {\overrightarrow {AC} ,\overrightarrow {B'D'} } \right) = \left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right) = 90^\circ ;\)
\(\left( {\overrightarrow {A'A} ,\overrightarrow {CB'} } \right) = \left( {\overrightarrow {C'C} ,\overrightarrow {CB'} } \right) = 180^\circ - \widehat {C'CB'} = 135^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo