III. Vận dụng
Một mảnh vườn hình chữ nhật có chiều dài \[30{\rm{\;m}},\] chiều rộng \[10\sqrt 3 {\rm{\;m}}.\] Khi đó góc giữa đường chéo và chiều dài của mảnh vườn bằng
A. \[30^\circ.\]
B. \[45^\circ.\]
C. \[60^\circ.\]
D. \[75^\circ.\]
Quảng cáo
Trả lời:
Đáp án đúng là: A
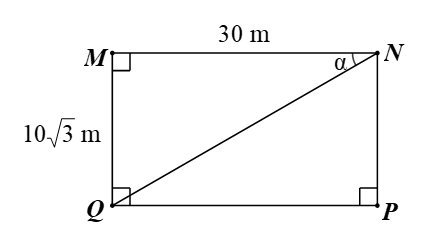
Gọi \[MNPQ\] là mảnh vườn hình chữ nhật và \[\alpha \] là góc giữa đường chéo \[NQ\] và chiều dài \[MN\] của mảnh vườn hình chữ nhật.
Vì tam giác \[MNQ\] vuông tại \[M\] nên \[\tan \alpha = \tan \widehat {MNQ} = \frac{{MQ}}{{MN}} = \frac{{10\sqrt 3 }}{{30}} = \frac{{\sqrt 3 }}{3}.\]
Sử dụng máy tính cầm tay, chuyển máy tính về chế độ “độ”, sau đó ấn liên tiếp các phím
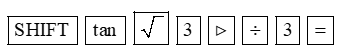
Màn hình hiện lên kết quả: \[30.\] Nghĩa là, \[\alpha = 30^\circ .\]
Do đó góc giữa đường chéo và chiều dài của mảnh vườn bằng \[30^\circ .\]
Vậy ta chọn phương án A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[\sin B = \tan C.\]
B. \[\tan B = \cos C.\]
C. \[\sin C = \cos B.\]
Lời giải
Đáp án đúng là: C
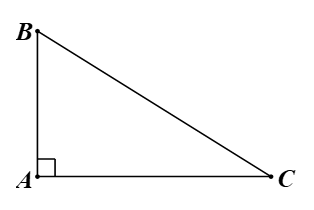
Cách 1. Do tam giác \[ABC\] vuông tại \[A\] nên
⦁ \[\sin B = \frac{{AC}}{{BC}}\] và \[\tan C = \frac{{AB}}{{AC}}.\] Suy ra \[\sin B \ne \tan C.\] Do đó phương án A sai.
⦁ \[\tan B = \frac{{AC}}{{AB}}\] và \[\cos C = \frac{{AC}}{{BC}}.\] Suy ra \[\tan B \ne \cos C.\] Do đó phương án B sai.
⦁ \[\sin C = \frac{{AB}}{{BC}}\] và \[\cos B = \frac{{AB}}{{BC}}.\] Suy ra \[\sin C = \cos B.\] Do đó phương án C đúng.
⦁ \[\cos B = \frac{{AB}}{{BC}}\] và \[\cos C = \frac{{AC}}{{BC}}.\]
Suy ra \[\frac{{\cos C}}{{\cos B}} = \frac{{AC}}{{BC}}:\frac{{AB}}{{BC}} = \frac{{AC}}{{BC}} \cdot \frac{{BC}}{{AB}} = \frac{{AC}}{{AB}} \ne \frac{{AB}}{{AC}}.\] Do đó phương án D sai.
Vậy ta chọn phương án C.
Cách 2. Vì tam giác \[ABC\] vuông tại \[A\] nên \(\widehat {B\,} + \widehat {C\,} = 90^\circ ,\) do đó hai góc \(B\) và \(C\) là hai góc phụ nhau.
Do đó \[\sin B = \cos C;\,\,\cos B = \sin C;\,\,\tan B = \cot C;\,\,\cot B = \tan C.\]
Vậy ta chọn phương án C.
Câu 2
A. \[J = 1.\]
B. \[J = 2.\]
C. \[J = 0.\]
D. \[J = 3.\]
Lời giải
Đáp án đúng là: C
⦁ Cách 1: Ta có: \[J = \tan 76^\circ - \cot 14^\circ = \tan 76^\circ - \cot \left( {90^\circ - 76^\circ } \right) = \tan 76^\circ - \tan 76^\circ = 0.\]
⦁ Cách 2: Sử dụng máy tính cầm tay:
Ta có: \[\cot 14^\circ = \frac{1}{{\tan 14^\circ }}.\]
Đầu tiên, ta đưa máy tính về chế độ “độ”, sau đó ấn liên tiếp các phím

Màn hình hiện lên kết quả: \[0.\] Nghĩa là, \[J = 0.\]
Vậy ta chọn phương án C.
Câu 3
A. Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \[\alpha ,\] kí hiệu \[\tan \alpha .\]
B. Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \[\alpha ,\] kí hiệu \[\sin \alpha .\]
C. Tỉ số giữa cạnh huyền và cạnh kề được gọi là côsin của góc \[\alpha ,\] kí hiệu \[\cot \alpha .\]
D. Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \[\alpha ,\] kí hiệu \[\cos \alpha .\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[2^\circ 9'.\]
B. \[2^\circ 8'.\]
C. \[87^\circ 52'.\]
D. \[87^\circ 51'.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[48^\circ.\]
B. \[49^\circ.\]
C. \[0^\circ.\]
D. \[1^\circ.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[I = 4.\]
B. \[I = 3.\]
C. \[I = 2.\]
D. \[I = 1.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.