Câu hỏi:
23/10/2024 2,871Một loại vi khuẩn sau mỗi phút số lượng tăng gấp đôi biết rằng sau 5 phút người ta đếm được có 64000 con. Hỏi sau bao nhiêu phút thì có được 2048000 con?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Số lượng vi khuẩn tăng sau mỗi phút lên là cấp số nhân \(\left( {{u_n}} \right)\) với công bội \(q = 2\). Ta có: \({u_6} = 64000 \Rightarrow {u_1}.{q^5} = 64000 \Rightarrow {u_1} = 2000\).
Sau \(n\) phút thì số lượng vi khuẩn là \({u_{n + 1}}\).
\({u_{n + 1}} = 2048000 \Rightarrow {u_1}.{q^n} = 2048000 \Rightarrow {2000.2^n} = 2048000 \Rightarrow n = 10.{\rm{ }}\)
Vậy sau 10 phút thì có được 2048000 con.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
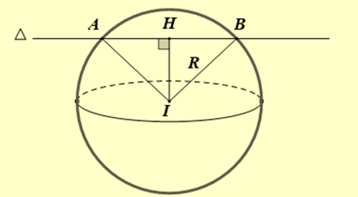
Gọi \(H\) là trung điểm đoạn thẳng \(AB \Rightarrow IH \bot AB,HA = 4\).
Mặt cầu \((S)\) có tâm \(I( - 2;3;0)\), bán kính \(R = \sqrt {13 - m} ,\,\,(m < 13)\).
Đường thẳng \(\Delta \) đi qua \(M(4;3;3)\) và có 1 vectơ chỉ phương \(\vec u = (2;1;2)\).
Ta có: \(\overrightarrow {IM} = (6;0;3) \Rightarrow [\overrightarrow {IM} ,\vec u] = ( - 3; - 6;6) \Rightarrow IH = d(I,\Delta ) = \frac{{\left| {\left[ {\overrightarrow {IM} ,\vec u} \right]} \right|}}{{|\vec u|}} = 3\)
\( \Rightarrow {R^2} = I{H^2} + H{A^2} \Leftrightarrow 13 - m = {3^2} + {4^2} \Leftrightarrow m = - 12\).
Vậy tham số \(m\) thuộc \(( - 15; - 5)\).
Lời giải
Đặt \(h = 5(m)\).
Gọi \({h_n}\) là độ cao (tính bằng mét) của quả bóng sau lần nảy lên thứ \(n\).
Lần nảy lên đầu tiên, quả bóng đạt độ cao \({h_1} = \frac{2}{3}h\).
Lần nảy lên thứ hai, quả bóng đạt độ cao \({h_2} = \frac{2}{3}{h_1}\).
Tương tự, lần nảy lên thứ \(n\), quả bóng đạt độ cao \({h_n} = \frac{2}{3}{h_{n - 1}}\).
\( \Rightarrow \) Tổng các quãng đường khi rơi và nảy của quả bóng từ lúc thả bóng cho đến lúc bóng không nảy lên nữa bằng tổng độ cao của của bóng khi nảy lên + tổng khoảng cách rơi xuống của quả bóng.
\( \Rightarrow T = \left( {h + {h_1} + {h_2} + \ldots + {h_n} + \ldots } \right) + \left( {{h_1} + {h_2} + \ldots + {h_n} + {h_{n + 1}} + \ldots } \right)\)
\( \Rightarrow T\) là tổng của hai cấp số nhân lùi vô hạn với số hạng đầu lần lượt là \(h\) và \({h_1}\); công bội \(q = \frac{2}{3}\).
\( \Rightarrow T = \frac{h}{{1 - \frac{2}{3}}} + \frac{{{h_1}}}{{1 - \frac{2}{3}}} = 3\left( {h + {h_1}} \right) = 3\left( {5 + \frac{2}{3}.5} \right) = 25(m){\rm{. }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 8)