Câu hỏi:
23/10/2024 57
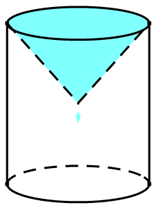
Đặt một chiếc phễu hình nón lên một chiếc cốc hình trụ như hình vẽ. Biết chiều cao của cốc bằng gấp đôi chiều cao của phễu. Giả sử độ dày thành cốc và phễu không đáng kể. Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng \(\frac{1}{2}\) chiều cao của phễu. Nước trong phễu sẽ chảy vào cốc qua lỗ nhỏ trên đỉnh phễu.
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu
Đúng
Sai
Thể tích của cốc gấp 4 lần thể tích phễu.
Khi nước trong phễu chảy hết vào cốc thì lượng nước trong cốc chiếm khoảng 2,08% thể tích cốc. (Coi như lượng nước không bị hao hụt và kết quả làm tròn đến chữ số thập phân thứ hai)
Nếu mỗi lần người ta chỉ đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng \(\frac{1}{2}\) chiều cao của phễu thì cần 12 lần đổ để chiều cao của nước trong cốc vừa chạm đỉnh phễu.
Đặt một chiếc phễu hình nón lên một chiếc cốc hình trụ như hình vẽ. Biết chiều cao của cốc bằng gấp đôi chiều cao của phễu. Giả sử độ dày thành cốc và phễu không đáng kể. Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng \(\frac{1}{2}\) chiều cao của phễu. Nước trong phễu sẽ chảy vào cốc qua lỗ nhỏ trên đỉnh phễu.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Thể tích của cốc gấp 4 lần thể tích phễu. |
||
|
Khi nước trong phễu chảy hết vào cốc thì lượng nước trong cốc chiếm khoảng 2,08% thể tích cốc. (Coi như lượng nước không bị hao hụt và kết quả làm tròn đến chữ số thập phân thứ hai) |
||
|
Nếu mỗi lần người ta chỉ đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng \(\frac{1}{2}\) chiều cao của phễu thì cần 12 lần đổ để chiều cao của nước trong cốc vừa chạm đỉnh phễu. |
Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Thể tích của cốc gấp 4 lần thể tích phễu. |
X | |
|
Khi nước trong phễu chảy hết vào cốc thì lượng nước trong cốc chiếm khoảng 2,08% thể tích cốc. (Coi như lượng nước không bị hao hụt và kết quả làm tròn đến chữ số thập phân thứ hai) |
X | |
|
Nếu mỗi lần người ta chỉ đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng 12 chiều cao của phễu thì cần 12 lần đổ để chiều cao của nước trong cốc vừa chạm đỉnh phễu. |
X |
Giải thích
Thể tích của cốc nước là: \[{V_0} = \pi {R^2}h\] .
Thể tích của phễu là: \({V_1} = \frac{1}{3}\pi {R^2}\frac{h}{2} = \frac{1}{6}{V_0}\).
Vậy thể tích của cốc gấp 6 lần thể tích phễu.
Vì lượng nước đổ vào phễu có chiều cao bằng \(\frac{1}{2}\) chiều cao của phễu nên bán kính của mặt nước là \(\frac{R}{2}\) (Áp dụng định lí Ta-let).
Khi đó, lượng nước đổ vào phễu là: \({V_2} = \frac{1}{3}\pi {\left( {\frac{R}{2}} \right)^2}.\frac{1}{2}.\frac{h}{2} = \frac{1}{{48}}{V_0} \approx 2,08\% {V_0}\)
⇒Chiều cao của nước trong cốc sau 1 lần đổ là \[\frac{h}{{48}}\].
Để để chiều cao của nước trong cốc vừa chạm đỉnh phễu thì cần \(\frac{h}{2}:\frac{h}{{48}} = 24\) lần đổ nước.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Định luật Newton II cho biết: “Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực tác dụng lên vật và tỉ lệ nghịch với khối lượng của vật”.
Ở thời điểm ban đầu, một chất điểm có khối lượng m = 1kg có vận tốc v0 = 20 m/s. Chất điểm chịu lực cản \({F_C} = - rv\) với r = ln2 và v là vận tốc của chất điểm tính bằng m/s. Sau 3s, chất điểm đạt vận tốc là
Định luật Newton II cho biết: “Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực tác dụng lên vật và tỉ lệ nghịch với khối lượng của vật”.
Ở thời điểm ban đầu, một chất điểm có khối lượng m = 1kg có vận tốc v0 = 20 m/s. Chất điểm chịu lực cản \({F_C} = - rv\) với r = ln2 và v là vận tốc của chất điểm tính bằng m/s. Sau 3s, chất điểm đạt vận tốc là
Xem đáp án »
23/10/2024
4,328
Câu 2:
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{\sqrt {x + 3} - m}}{{x - 1}}{\rm{ khi}}\,\,x \ne 1}\\{n\quad {\rm{ khi}}\,\,x = 1}\end{array}} \right.\). Để hàm số liên tục tại \({x_0} = 1\) thì giá trị của biểu thức \((m + n)\) tương ứng bằng
Xem đáp án »
23/10/2024
2,402
Câu 3:
Hãy điền một cụm từ không quá ba tiếng vào chỗ trống để hoàn thành nhận định sau:
Từ nền tảng ChatGPT đã được phát triển trước đó, một nhóm khởi nghiệp đã nghiên cứu và tìm ra phương thức giao tới với AI miễn phí thông qua (1) ________.
Hãy điền một cụm từ không quá ba tiếng vào chỗ trống để hoàn thành nhận định sau:
Từ nền tảng ChatGPT đã được phát triển trước đó, một nhóm khởi nghiệp đã nghiên cứu và tìm ra phương thức giao tới với AI miễn phí thông qua (1) ________.
Xem đáp án »
13/07/2024
1,274
Câu 4:
Hai bạn An và Bình chơi trò gieo xúc xắc với nhau. Luật chơi như sau: hai bạn có 3 con xúc xắc, các bạn gieo 3 con xúc xắc cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên (nếu có nhiều hơn 1 con xúc xắc cùng ra số chấm nhiều nhất thì bỏ ra 1 con xúc xắc bất kì trong đó), sau đó gieo 2 con xúc xắc còn lại cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên và gieo con xúc xắc còn lại, sau đó cộng số chấm trên 3 con xúc xắc đó với nhau, bạn nào có tổng số chấm cao hơn thì chiến thắng. Bạn An chơi trước, tổng số chấm trên 3 con xúc xắc bạn gieo được là 16. Xác suất bạn Bình giành chiến thắng là (1) _______ (viết kết quả dưới dạng phần trăm, làm tròn đến chữ số thập phân thứ nhất).
Hai bạn An và Bình chơi trò gieo xúc xắc với nhau. Luật chơi như sau: hai bạn có 3 con xúc xắc, các bạn gieo 3 con xúc xắc cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên (nếu có nhiều hơn 1 con xúc xắc cùng ra số chấm nhiều nhất thì bỏ ra 1 con xúc xắc bất kì trong đó), sau đó gieo 2 con xúc xắc còn lại cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên và gieo con xúc xắc còn lại, sau đó cộng số chấm trên 3 con xúc xắc đó với nhau, bạn nào có tổng số chấm cao hơn thì chiến thắng. Bạn An chơi trước, tổng số chấm trên 3 con xúc xắc bạn gieo được là 16. Xác suất bạn Bình giành chiến thắng là (1) _______ (viết kết quả dưới dạng phần trăm, làm tròn đến chữ số thập phân thứ nhất).
Xem đáp án »
23/10/2024
1,041
Câu 5:
Phần tư duy toán học
Cho khối lăng trụ tam giác đều ABC.A′B′C′ có chiều cao bằng \(a\sqrt 3 \) và hai đường thẳng AB′, BC′ vuông góc với nhau. Tính thể tích V của khối lăng trụ đã cho.
Xem đáp án »
23/10/2024
971
Câu 6:
Phần tư duy khoa học / giải quyết vấn đề
Hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí
quy mô quần thể, tốc độ sinh trưởng, thời gian kiếm ăn, tỉ lệ sinh sản/ tử vong
Theo nhà nghiên cứu 1, yếu tố _______ không thể theo dõi một cách dễ dàng ở loài chim biển.
Xem đáp án »
13/07/2024
933
Câu 7:
Virus nhận ra các tế bào chủ của nó theo nguyên tắc “chìa và khóa” nghĩa là
Xem đáp án »
30/06/2024
635
Bình luận
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 1)
-
ĐGTD ĐH Bách khoa - Sử dụng ngôn ngữ Tiếng Anh - Thì tương lai hoàn thành
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
ĐGTD ĐH Bách khoa - Sử dụng ngôn ngữ Tiếng Anh - Thì hiện tại đơn
-
Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2023 - 2024 có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
về câu hỏi!