Câu hỏi:
23/10/2024 1,280Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 4 . Hai mặt bên \((SAB)\) và \((SAD)\) cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng \((SCD)\) và \((ABCD)\) bằng \({45^o }\). Gọi \({V_1};{V_2}\) lần lượt là thể tích khối chóp S.AHK và S.ACD với H, K lần lượt là trung điểm của SC và SD. Độ dài đường cao của khối chóp S.ABCD là _______ và tỉ số \(k = \frac{{{V_1}}}{{{V_2}}} = \) _______.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 4 . Hai mặt bên \((SAB)\) và \((SAD)\) cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng \((SCD)\) và \((ABCD)\) bằng \({45^^\circ }\). Gọi \({V_1};{V_2}\) lần lượt là thể tích khối chóp S.AHK và S.ACD với H, K lần lượt là trung điểm của SC và SD. Độ dài đường cao của khối chóp S.ABCD là 4 và tỉ số \(k = \frac{{{V_1}}}{{{V_2}}} = \)\(\frac{1}{4}\) .
Giải thích
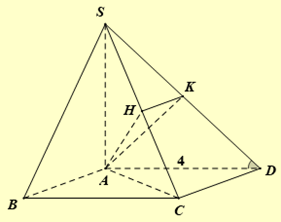
Do \((SAB)\) và \((SAD)\) cùng vuông góc với mặt đáy nên \(SA \bot (ABCD)\).
Ta có \(\left\{ {\begin{array}{*{20}{l}}{CD \bot AD}\\{CD \bot SA}\end{array} \Rightarrow CD \bot (SAD) \Rightarrow CD \bot SD} \right.\).
Dễ thấy góc giữa hai mặt phẳng \((SCD)\) và \((ABCD)\) là \(\widehat {SDA} = {45^o }\).
Ta có tam giác SAD là tam giác vuông cân đỉnh \(A\).
\( \Rightarrow h = SA = 4.{\rm{ }}\)
Áp dụng công thức tỉ số thể tích có: \(\frac{{{V_1}}}{{{V_2}}} = \frac{{SH}}{{SC}}.\frac{{SK}}{{SD}} = \frac{1}{4}\).
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi a là gia tốc của chất điểm.
Theo định luật II Newton ta có: \(a = \frac{F}{m} \Rightarrow {F_C} = ma = mv' = m\frac{{dv}}{{dt}}\).
Mà \({F_C} = - rv\) nên \( - rv = m\frac{{dv}}{{dt}} \Rightarrow \frac{{dv}}{v} = - \frac{r}{m}dt\)
\( \Leftrightarrow \int_{{v_0}}^v {\frac{{dv}}{v}} = \int_0^t - \frac{r}{m}dt \Leftrightarrow \ln \frac{v}{{{v_0}}} = - \frac{r}{m}t \Rightarrow v = {v_0}.{e^{ - \frac{r}{m}t}} = 2,5\,\,(m/s).\)
Chọn D
Lời giải
Đáp án
Hai bạn An và Bình chơi trò gieo xúc xắc với nhau. Luật chơi như sau: hai bạn có 3 con xúc xắc, các bạn gieo 3 con xúc xắc cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên (nếu có nhiều hơn 1 con xúc xắc cùng ra số chấm nhiều nhất thì bỏ ra 1 con xúc xắc bất kì trong đó), sau đó gieo 2 con xúc xắc còn lại cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên và gieo con xúc xắc còn lại, sau đó cộng số chấm trên 3 con xúc xắc đó với nhau, bạn nào có tổng số chấm cao hơn thì chiến thắng. Bạn An chơi trước, tổng số chấm trên 3 con xúc xắc bạn gieo được là 16. Xác suất bạn Bình giành chiến thắng là (1) __ 7,5% __ (viết kết quả dưới dạng phần trăm, làm tròn đến chữ số thập phân thứ nhất).
Giải thích
Tổng số chấm tối đa có thể thu được là 6.3 = 18.
Để bạn Bình giành chiến thắng thì tổng số chấm bạn thu được phải là 17hoặc 18.
TH1. Tổng số chấm là 18.
Để tổng số chấm là 18 thì con xúc xắc có số chấm nhiều nhất trong 3 lần gieo đều phải bằng 6.
Xác suất xảy ra là: \(\left[ {1 - {{\left( {\frac{5}{6}} \right)}^3}} \right].\left[ {1 - {{\left( {\frac{5}{6}} \right)}^2}} \right].\frac{1}{6} = \frac{{1001}}{{46656}}\).
TH2. Tổng số chấm là 17.
Để tổng số chấm là 17 thì con xúc xắc có số chấm nhiều nhất trong 2 lần gieo bằng 6, trong lần gieo còn lại bằng 5.
+ Số chấm cao nhất trong 3 lần gieo lần lượt là 6, 6, 5. Xác suất xảy ra là:
\(\left[ {1 - {{\left( {\frac{5}{6}} \right)}^3}} \right].\left[ {1 - {{\left( {\frac{5}{6}} \right)}^2}} \right].\frac{1}{6} = \frac{{1001}}{{46656}}\).
+ Số chấm cao nhất trong 3 lần gieo lần lượt là 6, 5, 6. Xác suất xảy ra là:
\(\left[ {1 - {{\left( {\frac{5}{6}} \right)}^3}} \right].\left( {C_2^1.\frac{1}{6}.\frac{4}{6} + \frac{1}{6}.\frac{1}{6}} \right).\frac{1}{6} = \frac{{91}}{{5184}}\).
+ Số chấm cao nhất trong 3 lần gieo lần lượt là 5, 6, 6. Xác suất xảy ra là:
\(\left[ {C_3^1.\frac{1}{6}.{{\left( {\frac{4}{6}} \right)}^2} + C_3^2.{{\left( {\frac{1}{6}} \right)}^2}.\frac{4}{6} + C_3^3.{{\left( {\frac{1}{6}} \right)}^3}} \right].\left[ {1 - {{\left( {\frac{5}{6}} \right)}^2}} \right].\frac{1}{6} = \frac{{671}}{{46656}}\) .
Xác suất để bạn Bình giành chiến thắng là:
\(\frac{{1001}}{{46656}} + \frac{{1001}}{{46656}} + \frac{{91}}{{5184}} + \frac{{671}}{{46656}} = \frac{{97}}{{1296}} \approx 7,5\% \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận