Câu hỏi:

23/10/2024 79

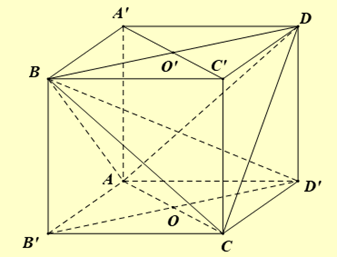
Cho tứ diện ABCD có $AB = CD = b,AC = BD = c,AD = BC = d$. Gọi $O,{O^\prime }$ lần lượt là trung điểm của ${\rm{AC}}$ và ${\rm{BD}}$. Dựng hai hình bình hành $AC{C^\prime }{A^\prime },BD{D^\prime }{B^\prime }$ sao cho ${A^\prime }{C^\prime }$ nhận ${O^\prime }$ làm trung điểm, ${B^\prime }{D^\prime }$ nhận ${\rm{O}}$ làm trung điểm. Nối các đoạn thẳng $A{A^\prime },B{B^\prime },C{C^\prime },D{D^\prime }$, ta thu được hình hộp $A{B^\prime }C{D^\prime }.{A^\prime }B{C^\prime }D$.

Các phát biểu dưới đây là đúng hay sai?

Phát biểu

Đúng

Sai

1) $A{B^\prime }C{D^\prime }.{A^\prime }B{C^\prime }D$ là hình hộp chữ nhật.

2) Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng $\pi \left( {{b^2} + {c^2} + {d^2}} \right)$.

3) Thể tích khối tứ diện ABCD bằng $\frac{{\sqrt {2\left( {{b^2} + {c^2} - {d^2}} \right)\left( {{b^2} - {c^2} + {d^2}} \right)\left( {{c^2} + {d^2} - {b^2}} \right)} }}{{12}}$.

Câu hỏi trong đề: Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 13) !!

Trả lời:

Giải bởi Vietjack

Đáp án

Phát biểu	Đúng	Sai
1) $A{B^\prime }C{D^\prime }.{A^\prime }B{C^\prime }D$ là hình hộp chữ nhật.	X
2) Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng $\pi \left( {{b^2} + {c^2} + {d^2}} \right)$.		X
3) Thể tích khối tứ diện ABCD bằng $\frac{{\sqrt {2\left( {{b^2} + {c^2} - {d^2}} \right)\left( {{b^2} - {c^2} + {d^2}} \right)\left( {{c^2} + {d^2} - {b^2}} \right)} }}{{12}}$.	X

Giải thích

$Cho tứ diện ABCD có $AB = CD = b,AC = BD = c,AD = BC = d$. Gọi $O,{O^\prime }$ lần lượt là trung điểm của ${\rm{AC}}$ và ${\rm{BD}}$. Dựng hai hình bình hành $AC{C^\prime }{A^\prime },BD{D^\prime }{B^\prime }$ sao cho ${A^\prime }{C^\prime }$ nhận ${O^\prime }$ làm trung điểm, ${B^\prime }{D^\prime }$ nhận ${\rm{O}}$ làm trung điểm. Nối các đoạn thẳng $A{A^\prime },B{B^\prime },C{C^\prime },D{D^\prime }$, ta thu được hình hộp $A{B^\prime }C{D^\prime }.{A^\prime }B{C^\prime }D$. Các phát biểu dưới đây là đúng hay sai? Phát biểu Đúng Sai 1) $A{B^\prime }C{D^\prime }.{A^\prime }B{C^\prime }D$ là hình hộp chữ nhật.   2) Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng $\pi \left( {{b^2} + {c^2} + {d^2}} \right)$.   3) Thể tích khối tứ diện ABCD bằng $\frac{{\sqrt {2\left( {{b^2} + {c^2} - {d^2}} \right)\left( {{b^2} - {c^2} + {d^2}} \right)\left( {{c^2} + {d^2} - {b^2}} \right)} }}{{12}}$.   (ảnh 1)$

Lí do lựa chọn phương án

1

Đúng vì:

Mỗi mặt của hình hộp là hình bình hành có hai đường chéo bằng nhau, do đó các mặt của hình hộp đều là những hình chữ nhật.

2

Sai vì:

Mặt cầu ngoại tiếp tứ diện ABCD có đường kính là $A{C^\prime } = \sqrt {{A^\prime }{A^2} + {A^\prime }{B^2} + {A^\prime }{D^2}} $

Vì $A{B^2} = {A^\prime }{B^2} + {A^\prime }{A^2};A{C^2} = {A^\prime }{B^2} + {A^\prime }{D^2};A{D^2} = {A^\prime }{A^2} + {A^\prime }{D^2}$

$ \Rightarrow 2\left( {{A^\prime }{A^2} + {A^\prime }{B^2} + {A^\prime }{D^2}} \right) = A{B^2} + A{C^2} + A{D^2}$

$ \Rightarrow A{C^\prime } = \sqrt {\frac{{{b^2} + {c^2} + {d^2}}}{2}} $

Suy ra diện tích của mặt cầu ngoại tiếp tứ diện ABCD bằng $4\pi {R^2} = \pi AC{'^2} = \frac{{\left( {{b^2} + {c^2} + {d^2}} \right)\pi }}{2}$.

3

Đúng vì:

Ta có ${V_{ABCD}} = \frac{1}{3}{V_{A{B^\prime }C{D^\prime }.{A^\prime }B{C^\prime }D}} = \frac{{{A^\prime }A.{A^\prime }B.{A^\prime }D}}{3}$

$ = \frac{{\sqrt {2\left( {{b^2} + {c^2} - {d^2}} \right)\left( {{b^2} - {c^2} + {d^2}} \right)\left( {{b^2} + {c^2} - {d^2}} \right)} }}{{12}}$.

Bình luận hoặc Báo cáo
về câu hỏi!

Câu 1:

Định luật Newton II cho biết: “Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực tác dụng lên vật và tỉ lệ nghịch với khối lượng của vật”.

Ở thời điểm ban đầu, một chất điểm có khối lượng m = 1kg có vận tốc v₀ = 20 m/s. Chất điểm chịu lực cản ${F_C} = - rv$ với r = ln2 và v là vận tốc của chất điểm tính bằng m/s. Sau 3s, chất điểm đạt vận tốc là

A. 2,1 m/s.

B. 4,3 m/s.

C. 4,6 m/s.

D. 2,5 m/s.

Xem đáp án » 23/10/2024 4,327

Câu 2:

Cho hàm số $f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{\sqrt {x + 3} - m}}{{x - 1}}{\rm{ khi}}\,\,x \ne 1}\\{n\quad {\rm{ khi}}\,\,x = 1}\end{array}} \right.$. Để hàm số liên tục tại ${x_0} = 1$ thì giá trị của biểu thức $(m + n)$ tương ứng bằng

A. $\frac{3}{4}$.

B. 1.

C. $ - \frac{1}{2}$.

D. $\frac{9}{4}$.

Xem đáp án » 23/10/2024 2,400

Câu 3:

Hãy điền một cụm từ không quá ba tiếng vào chỗ trống để hoàn thành nhận định sau:

Từ nền tảng ChatGPT đã được phát triển trước đó, một nhóm khởi nghiệp đã nghiên cứu và tìm ra phương thức giao tới với AI miễn phí thông qua (1) ________.

Xem đáp án » 13/07/2024 1,272

Câu 4:

Hai bạn An và Bình chơi trò gieo xúc xắc với nhau. Luật chơi như sau: hai bạn có 3 con xúc xắc, các bạn gieo 3 con xúc xắc cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên (nếu có nhiều hơn 1 con xúc xắc cùng ra số chấm nhiều nhất thì bỏ ra 1 con xúc xắc bất kì trong đó), sau đó gieo 2 con xúc xắc còn lại cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên và gieo con xúc xắc còn lại, sau đó cộng số chấm trên 3 con xúc xắc đó với nhau, bạn nào có tổng số chấm cao hơn thì chiến thắng. Bạn An chơi trước, tổng số chấm trên 3 con xúc xắc bạn gieo được là 16. Xác suất bạn Bình giành chiến thắng là (1) _______ (viết kết quả dưới dạng phần trăm, làm tròn đến chữ số thập phân thứ nhất).

Xem đáp án » 23/10/2024 1,041

Câu 5:

Phần tư duy toán học

Cho khối lăng trụ tam giác đều ABC.A′B′C′ có chiều cao bằng $a\sqrt 3 $ và hai đường thẳng AB′, BC′ vuông góc với nhau. Tính thể tích V của khối lăng trụ đã cho.

A. $6{a^3}$.

B. $\frac{5}{2}{a^3}$.

C. ${a^3}$.

D. $\frac{9}{2}{a^3}$.

Xem đáp án » 23/10/2024 971

Câu 6:

Phần tư duy khoa học / giải quyết vấn đề

Hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí

quy mô quần thể, tốc độ sinh trưởng, thời gian kiếm ăn, tỉ lệ sinh sản/ tử vong

Theo nhà nghiên cứu 1, yếu tố _______ không thể theo dõi một cách dễ dàng ở loài chim biển.

Xem đáp án » 13/07/2024 931

Câu 7:

Virus nhận ra các tế bào chủ của nó theo nguyên tắc “chìa và khóa” nghĩa là

A. protein bề mặt của virus có thể kết hợp được với nhiều thụ thể khác nhau của nhiều loại tế bào khác nhau.

B. protein bề mặt của virus liên kết đặc hiệu với từng loại thụ thể trên bề mặt tế bào.

C. protein bề mặt của virus mã hóa được mọi loại thụ thể tế bào.

D. protein bề mặt của virus liên kết không đặc hiệu với thụ thể trên bề mặt tế bào.

Xem đáp án » 30/06/2024 628

Xem thêm các câu hỏi khác »

Nhà sách VIETJACK:

Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{\sqrt {x + 3} - m}}{{x - 1}}{\rm{ khi}}\,\,x \ne 1}\\{n\quad {\rm{ khi}}\,\,x = 1}\end{array}} \right.\). Để hàm số liên tục tại \({x_0} = 1\) thì giá trị của biểu thức \((m + n)\) tương ứng bằng

Phần tư duy toán học

Cho khối lăng trụ tam giác đều ABC.A′B′C′ có chiều cao bằng \(a\sqrt 3 \) và hai đường thẳng AB′, BC′ vuông góc với nhau. Tính thể tích V của khối lăng trụ đã cho.

Virus nhận ra các tế bào chủ của nó theo nguyên tắc “chìa và khóa” nghĩa là

Bình luận

🔥 Đề thi HOT:

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

Phát biểu	Đúng	Sai
1) \(A{B^\prime }C{D^\prime }.{A^\prime }B{C^\prime }D\) là hình hộp chữ nhật.
2) Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng \(\pi \left( {{b^2} + {c^2} + {d^2}} \right)\).
3) Thể tích khối tứ diện ABCD bằng \(\frac{{\sqrt {2\left( {{b^2} + {c^2} - {d^2}} \right)\left( {{b^2} - {c^2} + {d^2}} \right)\left( {{c^2} + {d^2} - {b^2}} \right)} }}{{12}}\).

Nhà sách VIETJACK:

Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{\sqrt {x + 3} - m}}{{x - 1}}{\rm{ khi}}\,\,x \ne 1}\\{n\quad {\rm{ khi}}\,\,x = 1}\end{array}} \right.\). Để hàm số liên tục tại \({x_0} = 1\) thì giá trị của biểu thức \((m + n)\) tương ứng bằng

Phần tư duy toán học Cho khối lăng trụ tam giác đều ABC.A′B′C′ có chiều cao bằng \(a\sqrt 3 \) và hai đường thẳng AB′, BC′ vuông góc với nhau. Tính thể tích V của khối lăng trụ đã cho.

Virus nhận ra các tế bào chủ của nó theo nguyên tắc “chìa và khóa” nghĩa là

Bình luận

🔥 Đề thi HOT:

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Phần tư duy toán học

Cho khối lăng trụ tam giác đều ABC.A′B′C′ có chiều cao bằng \(a\sqrt 3 \) và hai đường thẳng AB′, BC′ vuông góc với nhau. Tính thể tích V của khối lăng trụ đã cho.