Câu hỏi:
24/10/2024 358
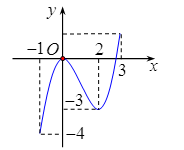
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị là đường cong trong hình vẽ bên. Tập hợp \(T\) là tập tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = m\) có 3 nghiệm phân biệt thuộc đoạn \(\left[ { - 1;3} \right]\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Giá trị nguyên nhỏ nhất của tập là _______.
Giá trị nguyên lớn nhất của tập là _______.
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị là đường cong trong hình vẽ bên. Tập hợp \(T\) là tập tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = m\) có 3 nghiệm phân biệt thuộc đoạn \(\left[ { - 1;3} \right]\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Giá trị nguyên nhỏ nhất của tập là _______.
Giá trị nguyên lớn nhất của tập là _______.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giá trị nguyên nhỏ nhất của tập \(T\) là -2 .
Giá trị nguyên lớn nhất của tập \(T\) là -1 .
Giải thích
Dựa vào đồ thị hàm số đã cho, phương trình \(f\left( x \right) = m\) có 3 nghiệm phân biệt thuộc đoạn \(\left[ { - 1;3} \right]\) thì \( - 3 < m < 0\) hay \(S = \left( { - 3;0} \right)\).
Vậy giá trị nguyên nhỏ nhất của tập \(T\) là -2 , giá trị nguyên lớn nhất của tập \(T\) là -1.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: “595”
Giải thích
Số đường chéo của đa giác là: \(C_{10}^2 - 10 = 35\).
Cứ hai đường chéo cho ta một giao điểm, hơn nữa không có ba đường chéo nào đồng quy nên số giao điểm của các đường chéo là \(C_{35}^2 = 595\).
Lời giải
Đáp án: “36/67”
Giải thích
Bước 1. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 8 .
Số phần tử không gian mẫu \(n\left( {\rm{\Omega }} \right) = 36\).
Để tổng số chấm xuất hiện trên hai con xúc xắc bằng 8 thì số chấm trên hai con xúc xắc là một trong các trường hợp sau \(\left( {2;6} \right),\left( {3;5} \right),\left( {4;4} \right),\left( {5;3} \right),\left( {6;2} \right)\).
Vậy xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 8 là \(\frac{5}{{36}}\).
Bước 2. Tính xác suất thắng của mỗi bạn.
\(A\) là biến cố bạn \({\rm{A}}\) là người chiến thắng.
\(P\left( A \right) = \left( {\frac{5}{{36}}} \right) + \left( {\frac{{31}}{{36}}.\frac{{31}}{{36}}.\frac{5}{{36}}} \right) + \left( {\frac{{31}}{{36}}.\frac{{31}}{{36}}.\frac{{31}}{{36}}.\frac{{31}}{{36}}.\frac{5}{{36}}} \right) + \ldots \)
\( = \frac{5}{{36}}\left[ {1 + {{\left( {\frac{{31}}{{36}}} \right)}^2} + {{\left( {\frac{{31}}{{36}}} \right)}^4} + \ldots } \right]\)
\( = \frac{5}{{36}}.\frac{1}{{1 - {{\left( {\frac{{31}}{{36}}} \right)}^2}}} = \frac{{36}}{{67}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 8)