Cho khối chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,N\) là hai điểm nằm trên hai cạnh \(SC,SD\) sao cho \(\frac{{SM}}{{SC}} = \frac{1}{2},\frac{{SN}}{{ND}} = 2\), biết G là trọng tâm tam giác \(SAB\). Tỉ số thể tích \(\frac{{{V_{G.MND}}}}{{{V_{S.ABCD}}}} = \frac{m}{n}\), \(m,n\) là các số nguyên dương và \(\left( {m,n} \right) = 1\). Giá trị của \(m + n\) bằng (1) ____
Cho khối chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,N\) là hai điểm nằm trên hai cạnh \(SC,SD\) sao cho \(\frac{{SM}}{{SC}} = \frac{1}{2},\frac{{SN}}{{ND}} = 2\), biết G là trọng tâm tam giác \(SAB\). Tỉ số thể tích \(\frac{{{V_{G.MND}}}}{{{V_{S.ABCD}}}} = \frac{m}{n}\), \(m,n\) là các số nguyên dương và \(\left( {m,n} \right) = 1\). Giá trị của \(m + n\) bằng (1) ____
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: “19”
Giải thích
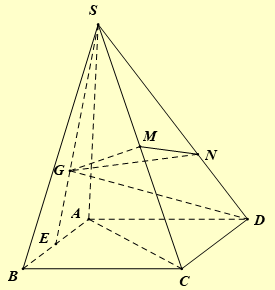
Ta có:
Gọi E là trung điểm của \(AB\).
\( \Rightarrow d\left( {G,\left( {DMN} \right)} \right) = \frac{2}{3}d\left( {{\rm{E}},\left( {DMN} \right)} \right) = \frac{2}{3}d\left( {{\rm{A}},\left( {DMN} \right)} \right) = \frac{2}{3}d\left( {{\rm{A}},\left( {SCD} \right)} \right)\)
\( \Rightarrow {V_{G.MND}} = \frac{1}{3}.{S_{{\rm{\Delta }}DMN}}.d\left( {G,\left( {DMN} \right)} \right)\)
\( \Rightarrow \frac{{{V_{G.MND}}}}{{{V_{S.ABCD}}}} = \frac{1}{{18}} \Rightarrow m + n = 19\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \({u_n} = {n^2}\).
B. \({u_n} = 2n\).
C. \({u_n} = {n^3} - 1\).
D. \({u_n} = \frac{{2n + 1}}{{n - 1}}\).
Lời giải
\(\forall n \in {\mathbb{N}^{\rm{*}}}\) ta có:
+ Với \({u_n} = {n^2}\) thì \({n^2} < {(n + 1)^2} \Leftrightarrow {u_n} < {u_{n + 1}} \Rightarrow {u_n} = {n^2}\) không là dãy số giảm.
+ Với \({u_n} = 2n\) thì \(2n < 2\left( {n + 1} \right) \Leftrightarrow {u_n} < {u_{n + 1}} \Rightarrow {u_n} = 2n\) không là dãy số giảm.
+ Với \({u_n} = {n^3} - 1\) thì \({n^3} - 1 < {(n + 1)^3} - 1 \Leftrightarrow {u_n} < {u_{n + 1}} \Rightarrow {u_n} = {n^3} - 1\) không là dãy số giảm.
+ Với \({u_n} = \frac{{2n + 1}}{{n - 1}}\) thì \({u_{n + 1}} - {u_n} = \frac{{ - 3}}{{\left( {n - 1} \right).n}} < 0\) nên dãy \({u_n} = \frac{{2n + 1}}{{n - 1}}\) là dãy số giảm.
Lời giải
Đáp án: “595”
Giải thích
Số đường chéo của đa giác là: \(C_{10}^2 - 10 = 35\).
Cứ hai đường chéo cho ta một giao điểm, hơn nữa không có ba đường chéo nào đồng quy nên số giao điểm của các đường chéo là \(C_{35}^2 = 595\).
Câu 3
A. sự rơi rụng từng đoạn NST, làm giảm số lượng gen trên NST.
B. sự trao đổi những đoạn NST không tương đồng làm thay đổi nhóm gen liên kết.
C. một đoạn NST đứt ra rồi đảo ngược 180o và nối lại làm thay đổi trình tự phân bố gen.
D. một đoạn của NST có thể lặp lại một hay nhiều lần, làm tăng số lượng gen trên đó.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Ảnh hưởng nghiêm trọng tới sức khỏe con người.
B. Mất đi cơ hội phát triển của cá nhân và đất nước.
C. Các dư chấn tâm lý do chịu căng thẳng kéo dài.
D. Tiêu tốn tài nguyên thiên nhiên, đặc biệt là chất đốt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập