Câu hỏi:
24/10/2024 1,581
Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai đường parabol có chung đinh, đối xứng với nhau qua trục của elip như hình vẽ. Biết độ dài trục lớn, trục nhỏ của elip lần lượt là 8m và 4m, F1, F2 lần lượt là hai tiêu điểm của elip. Phần A, B dùng để trồng hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ và 150.000 đ. Tính tồng số tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn).
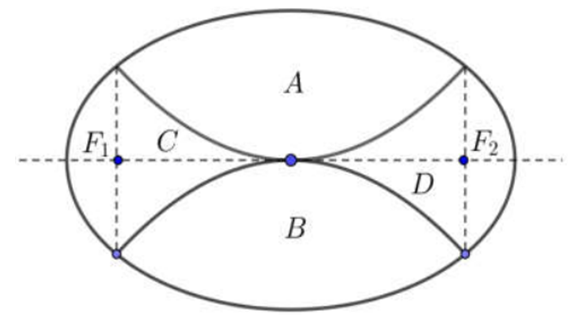
Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai đường parabol có chung đinh, đối xứng với nhau qua trục của elip như hình vẽ. Biết độ dài trục lớn, trục nhỏ của elip lần lượt là 8m và 4m, F1, F2 lần lượt là hai tiêu điểm của elip. Phần A, B dùng để trồng hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ và 150.000 đ. Tính tồng số tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp giải
Lời giải
Gọi SA, SB, SC, SD lần lượt là diện tích các phần A, B, C và D. Theo giả thiết ta được \[{S_A} = {S_B},\,\,{S_C} = {S_D}\].
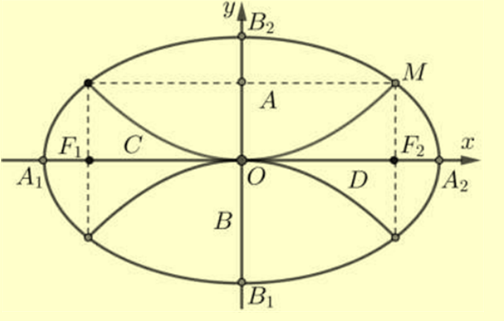
Chọn hệ tọa độ như hình vẽ. Khi đó elip \((E)\) có dạng \((E):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1,(0 < b < a)\).
Theo bài \(2a = 8 \Leftrightarrow a = 4;2b = 4 \Leftrightarrow b = 2\) suy ra phương trình của elip là
\((E):\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\) (1). \(c = \sqrt {{a^2} - {b^2}} = 2\sqrt 3 \) suy ra \({F_2}(2\sqrt 3 ;0)\).
Gọi \((P)\) là parabol nẳm ở phần phía trên của trục \({\rm{Ox}}\), cắt \((E)\) tại điểm \(M\) với hoành độ \({x_M} = 2\sqrt 3 \) khi đó \(M \in (E) \Rightarrow M(2\sqrt 3 ;1)\).
Theo giả thiết, parabol \((P)\) có dạng \(y = m.{x^2}\). Do \(M \in (P) \Rightarrow 1 = 12.m \Leftrightarrow m = \frac{1}{{12}}\).
Từ (1) ta được \(\frac{{{y^2}}}{4} = 1 - \frac{{{x^2}}}{{16}} \Leftrightarrow y = \pm \frac{1}{2}\sqrt {16 - {x^2}} \).
Diện tích của phần \(A\) là
\({S_A} = \int_{ - 2\sqrt 3 }^{2\sqrt 3 } {\left( {\frac{1}{2}\sqrt {16 - {x^2}} - \frac{1}{{12}}{x^2}} \right)} {\rm{d}}x = \int_{ - 2\sqrt 3 }^{2\sqrt 3 } {\frac{1}{2}} \sqrt {16 - {x^2}} \;{\rm{d}}x - \frac{1}{{12}}\int_{ - 2\sqrt 3 }^{2\sqrt 3 } {{x^2}} \;{\rm{d}}x{\rm{ hay}}\)
\({S_A} = {I_1} - \left. {\frac{1}{{36}}{x^3}} \right|_{ - 2\sqrt 3 }^{2\sqrt 3 } = {I_1} - \frac{{4\sqrt 3 }}{3}.\)
Với \({I_1} = \frac{1}{2}\int_{ - 2\sqrt 3 }^{2\sqrt 3 } {\sqrt {16 - {x^2}} } \;{\rm{d}}x\). Đặt \(x = 4\sin t \Rightarrow {\rm{d}}x = 4\cos t\;{\rm{d}}t\) với \(t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\).
Đổi cận: Khi \(x = - 2\sqrt 3 \) ta được \(t = - \frac{\pi }{3}\); khi \(x = 2\sqrt 3 \) ta được \(t = \frac{\pi }{3}\).
Theo công thức đổi biến số, thì:
\[{I_1} = \frac{1}{2}\int\limits_{ - \frac{\pi }{3}}^{\frac{\pi }{3}} {\sqrt {16 - 16{{\sin }^2}x} } .4\cos tdt = 8\int\limits_{ - \frac{\pi }{3}}^{\frac{\pi }{3}} {{{\cos }^2}} tdt\]
Hay \({I_1} = 4\int_{ - \frac{\pi }{3}}^{\frac{\pi }{3}} {(1 + \cos 2t)} dt = \left. {4\left( {t + \frac{1}{2}\sin 2t} \right)} \right|_{ - \frac{\pi }{3}}^{\frac{\pi }{3}} = 8\left( {\frac{\pi }{3} + \frac{{\sqrt 3 }}{4}} \right)\).
Từ đó tìm được \({S_A} = \frac{{8\pi + 2\sqrt 3 }}{3}\).
Diện tích của \((E)\) là \({S_{(E)}} = \pi ab = 8\pi \).
Diện tích của phần \(C\) là \({S_C} = {S_D} = \frac{{{S_{(E)}} - 2{S_A}}}{2} = \frac{{4\pi - 2\sqrt 3 }}{3}\).
Số tiền cần sử dụng để hoàn thành khu vườn trên là:
\(\left( {2.{S_A}} \right) \times 250000 + \left( {2.{S_C}} \right) \times 150000 \approx 5676367,372\)
Chọn A
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án
a) Nếu áp suất không khí ngoài máy bay bằng \(\frac{1}{2}{P_0}\) thì máy bay đang ở độ cao 5,84 km. (Làm tròn đến chữ số thập phân thứ hai)
b) Áp suất không khí tại đỉnh của ngọn núi A bằng \(\frac{4}{5}\) lần áp suất không khí tại đỉnh của ngọn núi B. Ngọn núi cao hơn là A, ngọn núi thấp hơn là B. Độ cao chênh lệch giữa hai ngọn núi là 1,88km. (Làm tròn đến chữ số thập phân thứ hai)
Phương pháp giải
Lời giải
a) Độ cao của máy bay khi áp suất không khí ngoài máy bay bằng \(\frac{1}{2}{P_0}\) là:
\(h = - 19,4.\log \frac{{\frac{1}{2}{P_0}}}{{{P_0}}} = - 19,4.\log \frac{1}{2} \approx 5,84\,\,({\rm{km}}).\)
b) Độ cao của ngọn núi A là: \({h_A} = - 19,4.\log \frac{{{P_A}}}{{{P_0}}}\).
Độ cao của ngọn núi B là: \({h_B} = - 19,4.\log \frac{{{P_B}}}{{{P_0}}}\).
Áp suất không khí tại đỉnh của ngọn núi \(A\) bằng \(\frac{4}{5}\) lần áp suất không khí tại đỉnh của ngọn núi \(B\) nên ta có:\({P_A} = \frac{4}{5}{P_B} \Leftrightarrow \frac{{{P_A}}}{{{P_B}}} = \frac{4}{5}{\rm{. }}\)
Ta có:
\(\begin{array}{l}{h_A} - {h_B} = \left( { - 19,4.\log \frac{{{P_A}}}{{{P_0}}}} \right) - \left( { - 19,4.\log \frac{{{P_B}}}{{{P_0}}}} \right) = - 19,4.\log \frac{{{P_A}}}{{{P_0}}} + 19,4.\log \frac{{{P_B}}}{{{P_0}}}\\ = - 19,4\log \left( {\frac{{{P_A}}}{{{P_0}}}:\frac{{{P_B}}}{{{P_0}}}} \right) = - 19,4\log \frac{{{P_A}}}{{{P_B}}} = - 19,4\log \frac{4}{5} \approx 1,88\,\,({\rm{km}}).\end{array}\)
Vậy ngọn núi \(A\) cao hơn ngọn núi \(B\) là \(1,88\;{\rm{km}}\).
Lời giải
Phương pháp giải
- Gọi h là chiều cao của hình trụ, biểu diễn h theo R.
- Biểu diễn diện tích toàn phần theo R.
- Sử dụng BĐT Cauchy để tìm giá trị min.
Diện tích hình trụ, thể tích khối trụ
Lời giải
Ta có 1000 lít = 1 m3.
Gọi h là chiều cao của hình trụ ta có \(K = \pi {R^2}h = 1 \Rightarrow h = \frac{1}{{\pi {R^2}}}\).
Diện tích toàn phần là: \({S_{tp}} = 2\pi {R^2} + 2\pi Rh = 2\pi {R^2} + 2\pi R\frac{1}{{\pi {R^2}}} = 2\pi {R^2} + \frac{2}{R}\)
\( = 2\left( {\pi {R^2} + \frac{1}{{2R}} + \frac{1}{{2R}}} \right) \ge 2.3\sqrt[3]{{\pi {R^2}.\frac{1}{{2R}}.\frac{1}{{2R}}}} = 6\sqrt[3]{{\frac{\pi }{4}}}\)
Dấu "=" xảy ra khi và chỉ khi \(\pi {R^2} = \frac{1}{{2R}} \Leftrightarrow R = \sqrt[3]{{\frac{1}{{2\pi }}}}\)
Chọn C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 8)