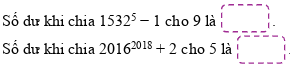Câu hỏi:
24/10/2024 374
Một bộ ba số Pythagoras (còn gọi là bộ ba số Pytago hay bộ ba số Pythagore) gồm ba số nguyên dương a, b và c, sao cho 
. Khi đó ta viết bộ ba đó là (a; b; c). Một bộ ba số Pythagoras được gọi là bộ ba số Pythagoras nguyên tố nếu a, b và c là các số nguyên tố cùng nhau.
Khẳng định nào sau đây đúng hay sai?
ĐÚNG
SAI
Bộ ba số (3; 4; 5) là bộ ba số Pytago nguyên tố
¡
¡
Hai số 153 và 185 có cùng thuộc 1 bộ ba số Pytago
¡
¡
Nếu (a; b; c) là bộ ba số Pytago, thì cả bộ ba (ka; kb; kc) với số nguyên k bất kỳ cũng là Pytago
¡
¡
Một bộ ba số Pythagoras (còn gọi là bộ ba số Pytago hay bộ ba số Pythagore) gồm ba số nguyên dương a, b và c, sao cho . Khi đó ta viết bộ ba đó là (a; b; c). Một bộ ba số Pythagoras được gọi là bộ ba số Pythagoras nguyên tố nếu a, b và c là các số nguyên tố cùng nhau.
Khẳng định nào sau đây đúng hay sai?
|
|
ĐÚNG |
SAI |
|
Bộ ba số (3; 4; 5) là bộ ba số Pytago nguyên tố |
¡ |
¡ |
|
Hai số 153 và 185 có cùng thuộc 1 bộ ba số Pytago |
¡ |
¡ |
|
Nếu (a; b; c) là bộ ba số Pytago, thì cả bộ ba (ka; kb; kc) với số nguyên k bất kỳ cũng là Pytago |
¡ |
¡ |
Câu hỏi trong đề:
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 7) !!
Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 49k/cuốn).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta thấy 52 = 32 + 42
Nên (3; 4; 5) là bộ ba số Pytago
Mà 3; 4; 5 có ước chung lớn nhất là 1 nên 3; 4; 5 là các số nguyên tố cùng nhau.
b)
TH1: Cả 2 số là các cạnh góc vuông
1532 + 1852 = 57634
Mà 57634 không là số chính phương nên loại
TH2: Có 1 số lớn nhất là cạnh huyền
1852 − 1532 = 1042 (thỏa mãn).
Hai số 153 và 185 có cùng thuộc 1 bộ ba số Pytago
c) Mệnh đề 3 sai vì với k = 0 thì (ka; kb; kc) không là bộ ba số Pytago.
Do đó ta chọn đáp án như sau
|
|
ĐÚNG |
SAI |
|
Bộ ba số (3; 4; 5) là bộ ba số Pytago nguyên tố |
¤ |
¡ |
|
Hai số 153 và 185 có cùng thuộc 1 bộ ba số Pytago |
¤ |
¡ |
|
Nếu (a; b; c) là bộ ba số Pytago, thì cả bộ ba (ka; kb; kc) với số nguyên k bất kỳ cũng là Pytago |
¡ |
¤ |
Nhà sách VIETJACK:
Sách - Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) cho 2k7 VietJack
Đã bán 902
₫ 150.000
₫ 39.000
Sách Combo - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) - 2024 cho 2k7 VietJack
Đã bán 1,4k
₫ 290.000
₫ 140.000
Sách - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) cho 2k7 VietJack
Đã bán 851
₫ 150.000
₫ 39.000
Sách Combo - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) - 2024 cho 2k7 VietJack
Đã bán 1,4k
₫ 280.000
₫ 150.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Phát biểu sau đây đúng hay sai?
Phản ứng với dung dịch NaOH chứng minh nhóm chức -OH phenol có lực acid mạnh hơn nhóm chức -OH alcohol.
Phát biểu sau đây đúng hay sai?
Phản ứng với dung dịch NaOH chứng minh nhóm chức -OH phenol có lực acid mạnh hơn nhóm chức -OH alcohol.
Xem đáp án »
24/10/2024
1,542
Câu 2:
Kéo các ô sau thả vào vị trí thích hợp để được khẳng định đúng:
Kéo các ô sau thả vào vị trí thích hợp để được khẳng định đúng:
Xem đáp án »
24/10/2024
1,199
Câu 3:
Truyện được kể theo ngôi kể nào? (Điền cụm từ thích hợp)
Truyện được kể theo ____________.
Truyện được kể theo ngôi kể nào? (Điền cụm từ thích hợp)
Truyện được kể theo ____________.
Xem đáp án »
24/10/2024
1,154
Câu 4:
Một người muốn mua một thanh gỗ đủ để cắt ra làm các thanh ngang của một cái thang. Biết rằng chiều dài các thanh ngang của cái thang đó (từ bậc dưới cùng) lần lượt là 45 cm, 43 cm , 41 cm,…,31 cm
Khẳng định nào đúng, khẳng định nào sai?
ĐÚNG
SAI
Cái thang đó có 8 bậc
¡
¡
Chiều dài thanh gỗ mà người đó cần mua là 304 cm, giả sử chiều dài các mối nối (phần gỗ bị cắt thành mùn cưa) là không đáng kể
¡
¡
Một người muốn mua một thanh gỗ đủ để cắt ra làm các thanh ngang của một cái thang. Biết rằng chiều dài các thanh ngang của cái thang đó (từ bậc dưới cùng) lần lượt là 45 cm, 43 cm , 41 cm,…,31 cm
Khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Cái thang đó có 8 bậc |
¡ |
¡ |
|
Chiều dài thanh gỗ mà người đó cần mua là 304 cm, giả sử chiều dài các mối nối (phần gỗ bị cắt thành mùn cưa) là không đáng kể |
¡ |
¡ |
Xem đáp án »
24/10/2024
1,063
Câu 5:
Giả sử có 12 viên bi khác màu nhau và 3 cái hộp, ta chia đều bi vào các hộp.
Kéo các ô sau thả vào vị trí thích hợp để được khẳng định đúng:
Xem đáp án »
24/10/2024
982
Câu 6:
Điền từ thích hợp vào chỗ trống:
Công suất hao phí do tỏa nhiệt trên đường dây dẫn điện tỉ lệ _______ với bình phương hiệu điện thế của hai đầu đường dây dẫn điện. Đồng thời, với cùng công suất, điệp áp truyền đi và điện trở đường dây, mạch có hệ số công càng _______ thì công suất hao phí càng nhỏ.
Điền từ thích hợp vào chỗ trống:
Công suất hao phí do tỏa nhiệt trên đường dây dẫn điện tỉ lệ _______ với bình phương hiệu điện thế của hai đầu đường dây dẫn điện. Đồng thời, với cùng công suất, điệp áp truyền đi và điện trở đường dây, mạch có hệ số công càng _______ thì công suất hao phí càng nhỏ.
Xem đáp án »
24/10/2024
661
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2023 - 2024 có đáp án (Đề 1)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 3)
-
Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2023 - 2024 có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận