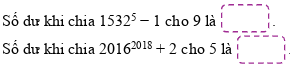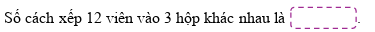Cho hàm số bậc ba  có đồ thị như hình vẽ bên. Số đường tiệm cận đứng của đồ thị hàm số
có đồ thị như hình vẽ bên. Số đường tiệm cận đứng của đồ thị hàm số  là:
là:

Cho hàm số bậc ba ![]() có đồ thị như hình vẽ bên. Số đường tiệm cận đứng của đồ thị hàm số
có đồ thị như hình vẽ bên. Số đường tiệm cận đứng của đồ thị hàm số  là:
là:

Quảng cáo
Trả lời:
Ta có: ![]() là hàm bậc 3, đồ thị cắt Ox tại các điểm
là hàm bậc 3, đồ thị cắt Ox tại các điểm  và tiếp xúc với trục Ox tại
và tiếp xúc với trục Ox tại ![]() .
.
Do đó 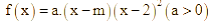
Đồ thị hàm số ![]() và
và ![]() cắt nhau tại 3 điểm phân biệt có hoành độ lần lượt là
cắt nhau tại 3 điểm phân biệt có hoành độ lần lượt là ![]()
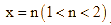 và
và 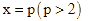 .
.
Do đó phương trình ![]() có các nghiệm là
có các nghiệm là 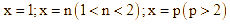 .
.
Ta được ![]() .
.
Từ đó ta có 
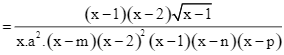 .
.
Ta có tập xác định của hàm ![]() là
là ![]() .
.
Từ hàm ![]() ta được đồ thị hàm số
ta được đồ thị hàm số ![]() có ba tiệm cận đứng:
có ba tiệm cận đứng:
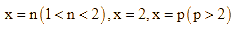 . Chọn B.
. Chọn B.Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có ![]()
Do đó ![]() .
.
Mà ![]() .
.
Do đó ![]() .
.
Vậy số dư cần tìm là 4 .
b) Ta có ![]() do đó
do đó ![]()
![]() .
.
Mà ![]() . Do đó
. Do đó ![]() .
.
Vậy số dư cần tìm là 3 .
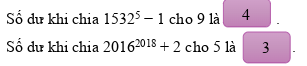
Lời giải
Chọn: Đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.