Câu hỏi:
24/10/2024 261
Cho hàm số \(y = {x^3} - \left( {m - 2} \right){x^2} + 3x - 1\left( C \right)\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Với \(m = 2\), đồ thị \(\left( C \right)\) có _______ điểm cực trị.
Có _______ giá trị nguyên âm của tham số \(m\) để đồ thị \(\left( C \right)\) cắt trục hoành tại đúng một điểm.
Cho hàm số \(y = {x^3} - \left( {m - 2} \right){x^2} + 3x - 1\left( C \right)\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:Với \(m = 2\), đồ thị \(\left( C \right)\) có _______ điểm cực trị.
Có _______ giá trị nguyên âm của tham số \(m\) để đồ thị \(\left( C \right)\) cắt trục hoành tại đúng một điểm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Với \(m = 2\), đồ thị \(\left( C \right)\) có 0 điểm cực trị.
Có 1 giá trị nguyên âm của tham số \(m\) để đồ thị \(\left( C \right)\) cắt trục hoành tại đúng một điểm.
Giải thích
Với \(m = 2\) ta có \(:y = {x^3} + 3x - 1 \Rightarrow y' = 3{x^2} + 3 > 0,\forall x \in \mathbb{R}\).
\( \Rightarrow \) Hàm số đã cho không có điểm cực trị.
Phương trình hoành độ giao điểm là : \({x^3} - \left( {m - 2} \right){x^2} + 3x - 1 = 0\,\,\left( {\rm{*}} \right)\).
Vì \(x = 0\) không là nghiệm của phương trình \(\left( {\rm{*}} \right)\) nên ta có :
\(\frac{{{x^3} + 3x - 1}}{{{x^2}}} = m - 2 \Leftrightarrow x + \frac{3}{x} - \frac{1}{{{x^2}}} = m - 2\).
Xét hàm số \(f\left( x \right) = x + \frac{3}{x} - \frac{1}{{{x^2}}} \Rightarrow f'\left( x \right) = 1 - \frac{3}{{{x^2}}} + \frac{2}{{{x^3}}} = \frac{{{x^3} - 3x + 2}}{{{x^3}}}\).
\(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = - 2}\end{array}} \right.\).
Bảng biến thiên :
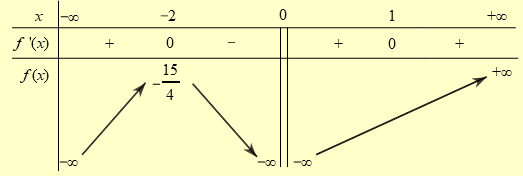
Dựa vào bảng biến thiên, ta thấy \(f\left( x \right) = m - 2\) có nghiệm duy nhất \( \Leftrightarrow m - 2 > - \frac{{15}}{4} \Leftrightarrow m > - \frac{7}{4}\).
Vậy có duy nhất một giá trị nguyên âm của tham số \(m\) để đồ thị hàm số \(\left( C \right)\) cắt trục hoành tại đúng một điểm.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
Phát biểu |
ĐÚNG |
SAI |
|
Với \(a = 1\) hàm số liên tục trái tại \(x = 1\). |
¤ |
¡ |
|
Với \(a = 1\) hàm số liên tục phải tại \(x = 1\). |
¡ |
¤ |
|
Với \(a = \pm 1\) hàm số liên tục tại \(x = 1\). |
¡ |
¤ |
Giải thích
Ta có: \(f(x) = \left\{ \begin{array}{l}x - 2\,\,khi\,\,x > 1\\a\,\,khi\,\,x = 1\\2 - x\,\,khi\,\,x < 1{\rm{\;}}\end{array} \right.\)
a) Để \(f\left( x \right)\) liên tục trái tại \(x = 1 \Leftrightarrow \mathop {{\rm{lim}}}\limits_{x \to {1^ - }} f\left( x \right)\) tồn tại và \(\mathop {{\rm{lim}}}\limits_{x \to {1^ - }} f\left( x \right) = f\left( 1 \right)\).
Ta có: \(\mathop {{\rm{lim}}}\limits_{x \to {1^ - }} f\left( x \right) = \mathop {{\rm{lim}}}\limits_{x \to {1^ - }} \left( {2 - x} \right) = 1\) và \(f\left( 1 \right) = a\).
Vậy với \(a = 1\) hàm số liên tục trái tại \(x = 1\).
b) Để \(f\left( x \right)\) liên tục phải tại \(x = 1 \Leftrightarrow \mathop {{\rm{lim}}}\limits_{x \to {1^ + }} f\left( x \right)\) tồn tại và \(\mathop {{\rm{lim}}}\limits_{x \to {1^ + }} f\left( x \right) = f\left( 1 \right)\).
Ta có: \(\mathop {{\rm{lim}}}\limits_{x \to {1^ + }} f\left( x \right) = \mathop {{\rm{lim}}}\limits_{x \to {1^ + }} \left( {x - 2} \right) = - 1\) và \(f\left( 1 \right) = a\).
Vậy với \(a = - 1\) hàm số liên tục phải tại \(x = 1\).
c) Do \(\mathop {{\rm{lim}}}\limits_{x \to {1^ - }} f\left( x \right) \ne \mathop {{\rm{lim}}}\limits_{x \to {1^ + }} f\left( x \right)\) nên hàm số không liên tục tại \(x = 1\).
Lời giải
Ánh sáng khả kiến là các bức xạ điện từ có bước sóng nằm trong vùng quang phổ nhìn thấy được bằng mắt thường của con người.
Chọn D
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận