Câu hỏi:
24/10/2024 2,531
Một nhà máy nhiệt điện sử dụng 90 máng Parabol thu nhiệt năng lượng mặt trời có cùng kích thước, bề mặt cong đều nhau. Mỗi máng có chiều rộng 2 m, bề dày của khối silic làm mặt máng là 2 dm, chiều dài 3 m. Đặt máng tiếp giáp mặt đất có điểm cao nhất của khối silic làm mặt máng so với mặt đất là 5 dm.
Khi đó thể tích của khối silic làm 90 mặt máng là
Một nhà máy nhiệt điện sử dụng 90 máng Parabol thu nhiệt năng lượng mặt trời có cùng kích thước, bề mặt cong đều nhau. Mỗi máng có chiều rộng 2 m, bề dày của khối silic làm mặt máng là 2 dm, chiều dài 3 m. Đặt máng tiếp giáp mặt đất có điểm cao nhất của khối silic làm mặt máng so với mặt đất là 5 dm.
Khi đó thể tích của khối silic làm 90 mặt máng là
Quảng cáo
Trả lời:
Giải bởi Vietjack
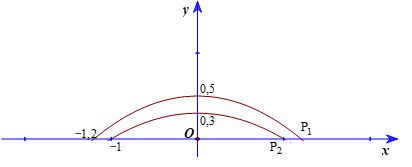
Gọi đường cong tương ứng với vành trên và vành dưới của máng lần lượt là 
và 
.
Xét hệ trục tọa độ Oxy như hình vẽ
Khi đó parabol và đều có dạng 
đi qua các điểm có tọa độ 
.
đi qua các điểm có tọa độ 
.
Suy ra 
và 
.
Diện tích mặt cắt của máng parabol là
.
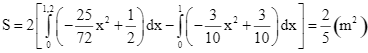Vậy thể tích của khối silic làm 90 mặt máng là 
. Chọn B.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Gọi hàm số bậc hai biểu thị độ cao 
theo thời gian 
là:
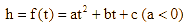. Theo giả thiết, quả bóng được đá lên từ mặt đất, nghĩa là 
, do đó 
.
Sau 2s, quả bóng lên đến vị trí cao nhất là 8m nên
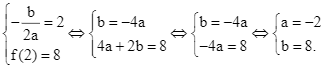
Vậy 
.
b) Độ cao của quả bóng sau khi đá lên được 3s là:
c) Cách 1. Quả bóng chạm đất (trở lại) khi độ cao h = 0, tức là:
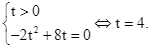
Vì thế sau 4s quả bóng sẽ chạm đất kể từ khi đá lên.
Cách 2. Quỹ đạo chuyển động của quả bóng là một phần của cung parabol có trục đối xứng là đường thẳng 
. Điểm xuất phát và điểm quả bóng chạm đất (trở lại) đối xứng nhau qua đường thẳng . Vì thế sau 
quả bóng sẽ chạm đất kể từ khi đá lên.
Do đó ta chọn đáp án như sau
|
|
ĐÚNG |
SAI |
|
Hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống này là |
¡ |
¤ |
|
Độ cao của quả bóng sau khi đá lên được 3s là 6m |
¤ |
¡ |
|
Sau 4 giây thì quả bóng chạm đất kể từ khi đá lên |
¤ |
¡ |
Lời giải
Áp dụng nguyên lý bất biến trong giải toán:
Cho a, b, c là những số thực ta xét tổng S = a + b + c . Nếu ta đổi chỗ a cho b, b cho c, c cho a, thì tổng S luôn luôn chỉ là một (không đổi). Tổng này không thay đổi đối với thứ tự phép cộng. Dù a, b, c có thay đổi thứ tự như thế nào chăng nữa S vẫn không thay đổi, nghĩa là S bất biến đối với việc thay đổi các biến khác.
Thông thường ta sẽ dựa vào kinh nghiệm dự đoán số bất biến trong dãy.
Nhận xét: c = a + b − 5ab là một tổng mà vai trò của a và b như nhau.
Cứ xóa 2 số a, b bất kì và xóa 2014 lần theo bất kì cách nào thì luôn ra một số duy nhất, nên ta có thể dự đoán: khi xóa đến một số nào đó thì số c là không đổi.
Giả sử xóa đến số a0 thì được số co = ao + b1 − 5a0b1
Xóa tiếp số co và b2 thì vẫn được co, tức là: co = co + b2 − 5cob2 ⇔ co = 
Thử lại ta thấy:
Trong dãy số trên có số 
.
Nếu xóa hai số a và b bất kì và thay bằng số mới là c = a + b − 5ab, như vậy sau mỗi lần xóa dãy trên giảm đi một số. Như vậy sau 2014 lần xóa trên bảng còn lại đúng 1 số.
Ta cứ xóa đến một lúc nào đó ta sẽ xóa 
và được thay bằng 
.
Như vậy cứ xóa số và một số b bất kì thì lại viết được c = .
Vậy số cuối cùng còn lại là .
Do đó ta điền đáp án như sau
Trên bảng viết các số 
. Mỗi lần biến đổi, xóa đi hai số 
bất kì và thay bằng số 
. Sau 2014 lần thực hiện phép biến đổi trên bảng còn lại một phân số 
. (tối giản)
Tổng m + n = 
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 8)