Câu hỏi:
25/10/2024 128
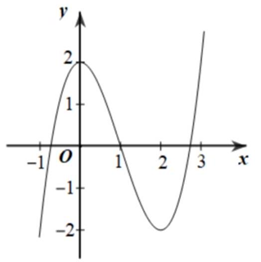
Cho hàm số bộc ba \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Đồ thị hàm số \(y = f\left( {x + a} \right)\) luôn có ______ điểm cực trị.
Đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) có ______ điểm cực trị.
Có ______ giá trị nguyên của tham số \(m\) để phương trình \(f\left( {{\rm{cos}}x} \right) = m\) có 3 nghiệm phân biệt thuộc khoảng \(\left( {0;\frac{{3\pi }}{2}} \right]\).
Cho hàm số bộc ba \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Đồ thị hàm số \(y = f\left( {x + a} \right)\) luôn có ______ điểm cực trị.
Đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) có ______ điểm cực trị.
Có ______ giá trị nguyên của tham số \(m\) để phương trình \(f\left( {{\rm{cos}}x} \right) = m\) có 3 nghiệm phân biệt thuộc khoảng \(\left( {0;\frac{{3\pi }}{2}} \right]\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
Đồ thị hàm số \(y = f\left( {x + a} \right)\) luôn có 2 điểm cực trị.
Đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) có 3 điểm cực trị.
Có 1 giá trị nguyên của tham số \(m\) để phương trình \(f\left( {{\rm{cos}}x} \right) = m\) có 3 nghiệm phân biệt thuộc khoảng \(\left( {0;\frac{{3\pi }}{2}} \right]\).
Giải thích
+) Tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) sang trái \(a\) đơn vị ta có đồ thị hàm số \(y = f\left( {x + a} \right)\). Vậy số điểm cực trị của đồ thị hàm số \(y = f\left( {x + a} \right)\) bằng số điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\). Hay đồ thị hàm số \(y = f\left( {x + a} \right)\) luôn có 2 điểm cực trị.
+) Số điểm cực trị đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) bằng \(2k + 1\) với \(k\) là số điểm cực trị dương của hàm số
\(y = f\left( x \right)\). Hay đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) có 3 điểm cực trị.
+) Đặt \(t = {\rm{cos}}x\) thì \(x \in \left( {0;\frac{{3\pi }}{2}} \right] \Rightarrow t \in \left[ { - 1;1} \right)\)
Với một nghiệm \(t \in \left( { - 1;0} \right]\) cho tương ứng được 2 nghiệm \(x \in \left[ {\frac{\pi }{2};\frac{{3\pi }}{2}} \right] \setminus \left\{ \pi \right\}\)
Với một nghiệm \(t \in \left( {0;1} \right) \cup \left\{ { - 1} \right\}\) cho tương ứng 1 nghiệm \(x \in \left( {0;\frac{\pi }{2}} \right) \cup \left\{ \pi \right\}\)
Do đó \(f\left( {{\rm{cos}}x} \right) = m\) có 3 nghiệm phân biệt thuộc khoảng \(\left( {0;\frac{{3\pi }}{2}} \right]\)
\( \Leftrightarrow f\left( t \right) = m\) có 2 nghiệm \({t_1} \in \left( { - 1;0} \right]\) và \({t_2} \in \left( {0;1} \right) \cup \left\{ { - 1} \right\}\)
Dựa vào đồ thị, ycbt \( \Leftrightarrow m \in \left( {0;2} \right)\).
Vì \(m \in \mathbb{Z}\) nên \(m = 1\) hay có 1 giá trị nguyên của tham số \(m\) thỏa mãn.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
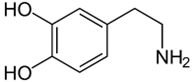
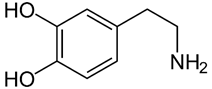
Theo đoạn văn: “Dopamine có công thức phân tử là C8H11NO2 (3,4-dihydroxyphenethylamine)” nên dopamine còn có tên gọi là 4-(2-aminoethyl)benzene-1,2-diol và công thức cấu tạo:
Chọn B
Lời giải
Theo bài đọc: “Dưới tác dụng của một số enzyme, tinh bột trong nông sản sẽ bị thủy phân tạo thành đường glucose.”
Chọn C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất