Câu hỏi:
25/10/2024 120
Trong không gian \(Oxyz\), cho các điểm \(A\left( {1;0;1} \right),B\left( {2;1;2} \right),C\left( {1; - 1;2} \right),D\left( {6; - 1;0} \right)\).
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu
Đúng
Sai
Mặt phẳng \(\left( {ABC} \right)\) có phương trình \(x - y - z = 0\).
Thể tích khối tứ diện \(ABCD\) bằng 2 đvtt.
Bán kính mặt cầu ngoại tiếp tứ diện \(ABCD\) bằng \(\frac{{\sqrt {53} }}{2}\).
Trong không gian \(Oxyz\), cho các điểm \(A\left( {1;0;1} \right),B\left( {2;1;2} \right),C\left( {1; - 1;2} \right),D\left( {6; - 1;0} \right)\).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Mặt phẳng \(\left( {ABC} \right)\) có phương trình \(x - y - z = 0\). |
||
|
Thể tích khối tứ diện \(ABCD\) bằng 2 đvtt. |
||
|
Bán kính mặt cầu ngoại tiếp tứ diện \(ABCD\) bằng \(\frac{{\sqrt {53} }}{2}\). |
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Mặt phẳng \(\left( {ABC} \right)\) có phương trình \(x - y - z = 0\). |
X | |
|
Thể tích khối tứ diện \(ABCD\) bằng 2 đvtt. |
X | |
|
Bán kính mặt cầu ngoại tiếp tứ diện \(ABCD\) bằng \(\frac{{\sqrt {53} }}{2}\). |
X |
Giải thích
Ta có: \(\overrightarrow {AB} = \left( {1;1;1} \right),\overrightarrow {AC} = \left( {0; - 1;1} \right) \Rightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {2; - 1; - 1} \right) = \vec n\).
Mặt phẳng \(\left( {ABC} \right)\) đi qua điểm \(A\left( {1;0;1} \right)\) và nhận \(\vec n = \left( {2; - 1; - 1} \right)\) làm một vecto pháp tuyến có phương trình: \(2\left( {x - 1} \right) - \left( {y - 0} \right) - \left( {z - 1} \right) = 0 \Leftrightarrow 2x - y - z - 1 = 0\).
Ta có: \(\overrightarrow {AD} = \left( {5; - 1; - 1} \right)\).
Thể tích khối tứ diện \(ABCD\) là:
\(V = \frac{1}{6}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} } \right| = \frac{1}{6}\left| {2.5 + \left( { - 1} \right).\left( { - 1} \right) + \left( { - 1} \right).\left( { - 1} \right)} \right| = 2\) (đvtt).
Ta thấy \(\overrightarrow {BD} = \left( {4; - 2; - 2} \right)//\vec n \Rightarrow BD \bot \left( {ABC} \right)\).
Mặt khác, vuông tại \(A\)
\( \Rightarrow \) Bán kính đường tròn ngoại tiếp là: \(r = \frac{{BC}}{2} = \frac{{\sqrt 5 }}{2}\).
\( \Rightarrow \) Bán kính mặt cầu ngoại tiếp tứ diện \(ABCD\) là:
\(R = \sqrt {{r^2} + \frac{{B{D^2}}}{4}} = \sqrt {{{\left( {\frac{{\sqrt 5 }}{2}} \right)}^2} + \frac{{{4^2} + {{( - 2)}^2} + {{( - 2)}^2}}}{4}} = \frac{{\sqrt {29} }}{2}\).
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
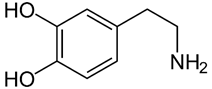
Theo đoạn văn: “Dopamine có công thức phân tử là C8H11NO2 (3,4-dihydroxyphenethylamine)” nên dopamine còn có tên gọi là 4-(2-aminoethyl)benzene-1,2-diol và công thức cấu tạo:
Chọn B
Lời giải
Theo bài đọc: “Dưới tác dụng của một số enzyme, tinh bột trong nông sản sẽ bị thủy phân tạo thành đường glucose.”
Chọn C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận