Câu hỏi:
25/10/2024 180
Cho hàm số \(y = f\left( x \right)\) liên tục và nhận giá trị không âm trên đoạn \(\left[ {a;b} \right]\). Cho tấm phẳng T có mật độ đều và chiếm một miền \(R\) được giới hạn bởi trục hoành, hai đường thẳng \(x = a,x = b\) và đồ thị hàm số \(y = f\left( x \right)\). Trọng tâm của T là điểm \(C\left( {\overline x ;\overline y } \right)\) có tọa độ được xác định bởi công thức:
\(\overline x = \frac{1}{A}\int\limits_a^b {xf\left( x \right){\rm{d}}x} ,\) \(\overline {\rm{y}} = \frac{1}{A}\int\limits_a^b {\frac{1}{2}{f^2}\left( x \right){\rm{d}}x} \)
với \(A\) là diện tích của miền \(R\).
Cho tấm phẳng \({\rm{T}}\) có dạng hình bán nguyệt như hình dưới đây có bán kính bằng \(6\pi \) (đơn vị), \(AB\) là đường kính, \(O\) là trung điểm của \(AB\) và \(IO\) vuông góc với \(AB\) tại \(O\).
![Cho hàm số \(y = f\left( x \right)\) liên tục và nhận giá trị không âm trên đoạn \(\left[ {a;b} \right]\). Cho tấm phẳng T có mật độ đều và chiếm một miền \(R\) được giới hạn bởi trục hoành, hai đường thẳng \(x = a,x = b\) và đồ thị hàm số \(y = f\left( x \right)\). Trọng tâm của T là điểm \(C\left( {\overline x ;\overline y } \right)\) có tọa độ được xác định bởi công thức: \(\overline x = \frac{1}{A}\int\limits_a^b {xf\left( x \right){\rm{d}}x} ,\) \(\overline {\rm{y}} = \frac{1}{A}\int\limits_a^b {\frac{1}{2}{f^2}\left( x \right){\rm{d}}x} \) với \(A\) là diện tích của miền \(R\). Cho tấm phẳng \({\rm{T}}\) có dạng hình bán nguyệt như hình dưới đây có bán kính bằng \(6\pi \) (đơn vị), \(AB\) là đường kính, \(O\) là trung điểm của \(AB\) và \(IO\) vuông góc với \(AB\) tại \(O\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid18-1729827342.png)
Kéo số thích hợp ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
![Cho hàm số \(y = f\left( x \right)\) liên tục và nhận giá trị không âm trên đoạn \(\left[ {a;b} \right]\). Cho tấm phẳng T có mật độ đều và chiếm một miền \(R\) được giới hạn bởi trục hoành, hai đường thẳng \(x = a,x = b\) và đồ thị hàm số \(y = f\left( x \right)\). Trọng tâm của T là điểm \(C\left( {\overline x ;\overline y } \right)\) có tọa độ được xác định bởi công thức: \(\overline x = \frac{1}{A}\int\limits_a^b {xf\left( x \right){\rm{d}}x} ,\) \(\overline {\rm{y}} = \frac{1}{A}\int\limits_a^b {\frac{1}{2}{f^2}\left( x \right){\rm{d}}x} \) với \(A\) là diện tích của miền \(R\). Cho tấm phẳng \({\rm{T}}\) có dạng hình bán nguyệt như hình dưới đây có bán kính bằng \(6\pi \) (đơn vị), \(AB\) là đường kính, \(O\) là trung điểm của \(AB\) và \(IO\) vuông góc với \(AB\) tại \(O\). (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid17-1729827328.png)
1) Diện tích của tấm phẳng \({\rm{T}}\) là _______ (đơn vị diện tích).
2) Trọng tâm của T nằm trên đoạn thẳng _______.
3) Khoảng cách từ trọng tâm đến \({\rm{O}}\) là _______ (đơn vị độ dài).
Cho hàm số \(y = f\left( x \right)\) liên tục và nhận giá trị không âm trên đoạn \(\left[ {a;b} \right]\). Cho tấm phẳng T có mật độ đều và chiếm một miền \(R\) được giới hạn bởi trục hoành, hai đường thẳng \(x = a,x = b\) và đồ thị hàm số \(y = f\left( x \right)\). Trọng tâm của T là điểm \(C\left( {\overline x ;\overline y } \right)\) có tọa độ được xác định bởi công thức:
\(\overline x = \frac{1}{A}\int\limits_a^b {xf\left( x \right){\rm{d}}x} ,\) \(\overline {\rm{y}} = \frac{1}{A}\int\limits_a^b {\frac{1}{2}{f^2}\left( x \right){\rm{d}}x} \)
với \(A\) là diện tích của miền \(R\).
Cho tấm phẳng \({\rm{T}}\) có dạng hình bán nguyệt như hình dưới đây có bán kính bằng \(6\pi \) (đơn vị), \(AB\) là đường kính, \(O\) là trung điểm của \(AB\) và \(IO\) vuông góc với \(AB\) tại \(O\).
Kéo số thích hợp ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
1) Diện tích của tấm phẳng \({\rm{T}}\) là _______ (đơn vị diện tích).
2) Trọng tâm của T nằm trên đoạn thẳng _______.
3) Khoảng cách từ trọng tâm đến \({\rm{O}}\) là _______ (đơn vị độ dài).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
1) Diện tích của tấm phẳng \({\rm{T}}\) là \(18{\pi ^3}\) (đơn vị diện tích).
2) Trọng tâm của T nằm trên đoạn thẳng IO.
3) Khoảng cách từ trọng tâm đến \({\rm{O}}\) là 8 (đơn vị độ dài).
Giải thích
|
Lí do lựa chọn phương án
|
Vị trí thả 1 |
Diện tích hình bán nguyệt là \(A = \frac{1}{2}\pi {r^2} = 18{\pi ^3}\) (đơn vị diện tích). |
|
Vị trí thả 2
|
Đưa hình bán nguyệt lên mặt phẳng tọa độ có \({\rm{O}}\) trùng gốc tọa tọa độ, Oy trùng với \({\rm{AB}},{\rm{Ox}}\) trùng với OI. Khi đó cung \({\rm{AB}}\) có phương trình là \(y = \sqrt {{r^2} - {x^2}} \). Vận dụng công thức xác định tọa độ trọng tâm ta có: \(\overline x = \frac{1}{A}\int\limits_{ - r}^r {xf\left( x \right)dx = 0} \) Nên trọng tâm của T nằm trên IO. |
|
|
Vị trí thả 3
|
Vận dụng công thức xác định tọa độ trọng tâm ta có: \(\overline y = \frac{1}{A}\int\limits_{ - r}^r {\frac{1}{2}{f^2}\left( x \right)dx} = \frac{{4r}}{{3\pi }} = 8\) (đơn vị độ dài) Nên khoảng cách từ trọng tâm đến O bằng 8 đơn vị độ dài. |
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
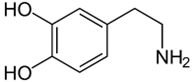
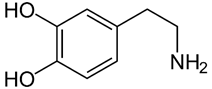
Theo đoạn văn: “Dopamine có công thức phân tử là C8H11NO2 (3,4-dihydroxyphenethylamine)” nên dopamine còn có tên gọi là 4-(2-aminoethyl)benzene-1,2-diol và công thức cấu tạo:
Chọn B
Lời giải
Theo bài đọc: “Dưới tác dụng của một số enzyme, tinh bột trong nông sản sẽ bị thủy phân tạo thành đường glucose.”
Chọn C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận