Câu hỏi:
30/10/2024 798
Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thoi cạnh \(2,\widehat {BAD} = {120^ \circ }\). Biết các đường thẳng \(A'A,A'B,A'C\) cùng tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc bằng \({60^ \circ }\). Gọi \(M,N\) lần lượt là trung điểm của \(BB',CC'\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
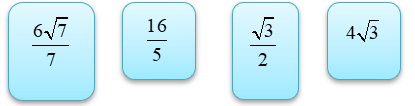
Thể tích khối lăng trụ \(ABCD.A'B'C'D'\) bằng _______.
Khoảng cách giữa \(AD\) và mặt phẳng \(\left( {D'MN} \right)\) bằng _______.
Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thoi cạnh \(2,\widehat {BAD} = {120^ \circ }\). Biết các đường thẳng \(A'A,A'B,A'C\) cùng tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc bằng \({60^ \circ }\). Gọi \(M,N\) lần lượt là trung điểm của \(BB',CC'\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau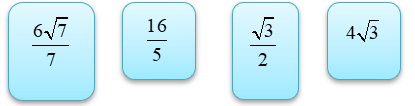Thể tích khối lăng trụ \(ABCD.A'B'C'D'\) bằng _______.
Khoảng cách giữa \(AD\) và mặt phẳng \(\left( {D'MN} \right)\) bằng _______.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
Thể tích khối lăng trụ \(ABCD.A'B'C'D'\) bằng \(4\sqrt 3 \).
Khoảng cách giữa \(AD\) và mặt phẳng \(\left( {D'MN} \right)\) bằng \(\frac{{6\sqrt 7 }}{7}\).
Giải thích
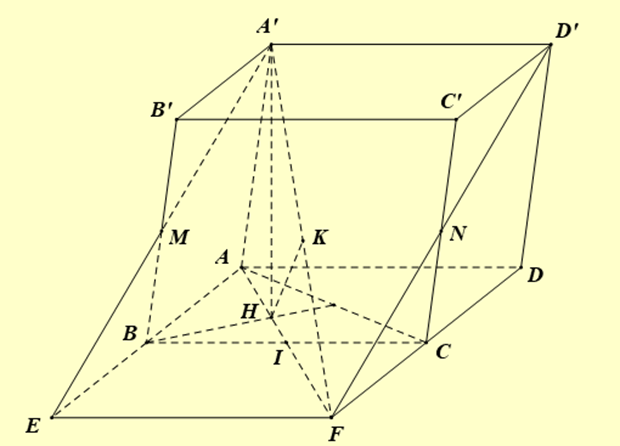
Vị trí thả 1: \(4\sqrt 3 \)
Vị trí thả 2: \(\frac{{6\sqrt 7 }}{7}\)
Tính thể tích khối lăng trụ \(ABCD.A'B'C'D'\).
Gọi \(I\) là trung điểm của \(BC\).
Gọi \(H\) là hình chiếu vuông góc của điểm \(A'\) trên mặt phẳng \(\left( {ABCD} \right)\) vì các đường thẳng \(A'A\), \(A'B,A'C\) cùng tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc bằng \({60^ \circ }\) nên \[\widehat {HAA'} = \widehat {HBA'} = \widehat {HCA'} = {60^ \circ }\].
\( \Rightarrow {\rm{\Delta }}A'HA = {\rm{\Delta }}A'HB = {\rm{\Delta }}A'HC\) (g.c.g) \( \Rightarrow HA = HB = HC\).
\( \Rightarrow H\) là tâm đường tròn ngoại tiếp .
Vì \(ABCD\) là hình thoi có \(\widehat {BAD} = {120^ \circ }\)
\( = > \widehat {\left( {BAC} \right)} = {60^0} \Rightarrow \Delta ABC\) đều
\( \Rightarrow H\) là trọng tâm .
Ta có \(AI = \frac{{2.\sqrt 3 }}{2} = \sqrt 3 \Rightarrow AH = \frac{{2\sqrt 3 }}{3} \Rightarrow A'H = AH{\rm{tan}}\widehat {A'AH} = 2\),
\({S_{ABCD}} = AB.AD.{\rm{sin}}\widehat {BAD} = \frac{{{2^2}\sqrt 3 }}{2} = 2\sqrt 3 \).
Thể tích khối lăng trụ \(ABCD.A'B'C'D'\) là \(V = A'H.{S_{ABCD}} = \frac{{{2^3}\sqrt 3 }}{2} = 4\sqrt 3 \).
Tính khoảng cách giữa đường thẳng \(AD\) và mặt phẳng \(\left( {D'MN} \right)\)
Do \(MN//A'D'\) nên \(A'\) thuộc mặt phẳng \(\left( {D'MN} \right)\)
Gọi \(E = A'M \cap AB,F = D'N \cap DC \Rightarrow EF//BC//AD\) và \(B,C\) lần lượt là trung điểm của các đoạn thẳng \(AE,DF\). Suy ra \(A,H,F\) thẳng hàng và \(AF = \frac{3}{2}HF\).
Ta có \(AD//\left( {D'MN} \right) \Rightarrow d\left( {AD,\left( {D'MN} \right)} \right) = d\left( {A,\left( {A'EF} \right)} \right) = \frac{3}{2}d\left( {H,\left( {A'EF} \right)} \right)\).
Do \(AH \bot BC \Rightarrow AH \bot EF \Rightarrow EF \bot \left( {A'HF} \right) \Rightarrow \left( {A'EF} \right) \bot \left( {A'HF} \right)\)
Trong tam giác \(A'HF\), kẻ \(HK \bot A'F \Rightarrow HK \bot \left( {A'EF} \right) \Rightarrow d\left( {H,\left( {A'EF} \right)} \right) = HK\)
Ta có \(A'H = 2,HF = 2HA = \frac{{4\sqrt 3 }}{3},\frac{1}{{H{K^2}}} = \frac{1}{{HA{'^2}}} + \frac{1}{{H{F^2}}} = \frac{1}{4} + \frac{3}{{16}} = \frac{7}{{16}} \Rightarrow HK = \frac{{4\sqrt 7 }}{7}\).
\( \Rightarrow d\left( {AD,\left( {D'MN} \right)} \right) = \frac{3}{2}HK = \frac{{6\sqrt 7 }}{7}\).
Nhà sách vietjack
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Một lớp học trong một trường đại học có 60 sinh viên, trong đó có 40 sinh viên học tiếng Anh, 30 sinh viên học tiếng Pháp và 20 sinh viên học cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên 2 sinh viên của lớp học này. Tính xác suất để 2 sinh viên được chọn không học ngoại ngữ. Biết rằng trường này chỉ dạy hai loại ngoại ngữ là tiếng Anh và tiếng Pháp.
Một lớp học trong một trường đại học có 60 sinh viên, trong đó có 40 sinh viên học tiếng Anh, 30 sinh viên học tiếng Pháp và 20 sinh viên học cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên 2 sinh viên của lớp học này. Tính xác suất để 2 sinh viên được chọn không học ngoại ngữ. Biết rằng trường này chỉ dạy hai loại ngoại ngữ là tiếng Anh và tiếng Pháp.
Xem đáp án »
30/10/2024
2,153
Câu 3:
Phát biểu sau đúng hay sai?
Ethylene có công thức cấu tạo: H−C≡C−H. Trong phân tử ethylene có một liên kết ba giữa hai nguyên tử carbon.
Phát biểu sau đúng hay sai?
Ethylene có công thức cấu tạo: H−C≡C−H. Trong phân tử ethylene có một liên kết ba giữa hai nguyên tử carbon.
Xem đáp án »
02/07/2024
2,023
Câu 4:
Phần tư duy khoa học / giải quyết vấn đề
Phát biểu sau đây đúng hay sai?
Lực tương tác giữa proton và electron được gọi là lực hút tĩnh điện.
Xem đáp án »
02/07/2024
1,614
Câu 5:
Trong công nghệ “tàu đệm từ” EDS, các nam châm trên tàu được đặt ở
Xem đáp án »
02/07/2024
1,567
Câu 7:
Trong không gian \(Oxyz\), cho hai mặt phẳng \(\left( P \right):x + 4y - 2z - 6 = 0\) và \(\left( Q \right):x - 2y + 4z - 6 = 0\). Gọi \(\left( \alpha \right)\) là mặt phẳng chứa giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\) đồng thời cắt các trục tọa độ tại các điểm \(A,B,C\) sao cho hình chóp \(O.ABC\) đều. Phương trình mặt phẳng \(\left( \alpha \right)\) là
Xem đáp án »
30/10/2024
1,445
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 15)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 3)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 5)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận