Trong không gian 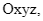 cho hai mặt phẳng
cho hai mặt phẳng 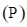 và
và 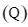 cùng thỏa mãn các điều kiện sau: đi qua hai điểm
cùng thỏa mãn các điều kiện sau: đi qua hai điểm 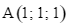 và
và 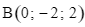 , đồng thời cắt các trục tọa độ
, đồng thời cắt các trục tọa độ 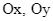 tại hai điểm cách đều O. Giả sử
tại hai điểm cách đều O. Giả sử 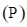 có phương trình
có phương trình 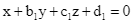 và
và 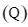 có phương trình
có phương trình 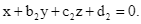 Giá trị của biểu thức
Giá trị của biểu thức 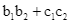 bằng:
bằng:
Quảng cáo
Trả lời:
Xét mặt phẳng ![]() có phương trình
có phương trình ![]() đi qua hai điểm
đi qua hai điểm ![]() và
và ![]() , đồng thời cắt các trục tọa độ
, đồng thời cắt các trục tọa độ ![]() tại hai điểm cách đều.
tại hai điểm cách đều.
Vì ![]() đi qua
đi qua ![]() và
và ![]() nên ta có hệ phương trình:
nên ta có hệ phương trình: 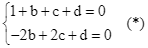
Mặt phẳng ![]() cắt các trục tọa độ
cắt các trục tọa độ ![]() lần lượt tại
lần lượt tại ![]()
Vì ![]() cách đều
cách đều ![]() nên
nên ![]() Suy ra:
Suy ra: ![]()
Nếu ![]() thì chỉ tồn tại hai mặt phẳng thỏa mãn yêu cầu bài toán (mặt phẳng này đi qua điểm O).
thì chỉ tồn tại hai mặt phẳng thỏa mãn yêu cầu bài toán (mặt phẳng này đi qua điểm O).
Do đó để tồn tại hai mặt phẳng thỏa mãn yêu cầu bài toán thì: ![]()
Với ![]() thì
thì 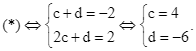 Ta được mặt phẳng
Ta được mặt phẳng ![]() .
.
Với 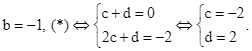 Ta được mặt phẳng
Ta được mặt phẳng ![]() .
.
Vậy ![]() Chọn B.
Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: ![]() .
.
Và ![]() .
.
Gia tốc của chất điểm tại thời điểm ![]() là:
là:
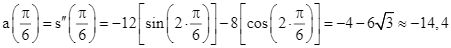 .
.
Đáp án cần nhập là: ![]() .
.
Lời giải
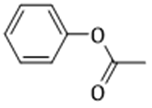
Ester là ![]() (phenyl ethanoate hay phenyl acetate).
(phenyl ethanoate hay phenyl acetate).
Phát biểu (a) sai, vì: Tên của ester là phenyl ethanoate.
Phát biểu (b) sai, vì: ![]()
Phát biểu (c) sai, vì: Ester trên không được điều chế từ phản ứng ester hóa giữa phenol và acetic acid.
Phát biểu (d) đúng, vì: Ester trên có công thức phân tử ![]() với công thức đơn giản nhất là
với công thức đơn giản nhất là ![]()
Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.