Câu hỏi:
12/11/2024 362
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình bên.
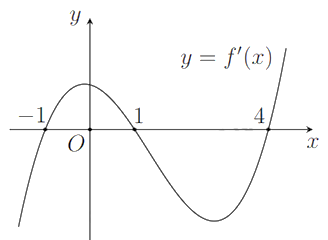
Khẳng định nào sau đây sai?
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình bên.
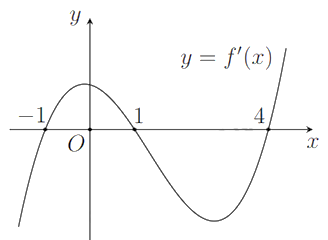
Khẳng định nào sau đây sai?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
B. Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
C. \(f\left( { - 1} \right) < f\left( 4 \right) < f\left( 1 \right)\).
Xét từng mệnh đề.
- Số cực trị của \(y = f\left( x \right)\)
- Hàm số \(y = f\left( x \right)\) đồng biến trên những khoảng mà \(f'\left( x \right) > 0\).
- Tính tích phân từ - 1 đến 1 , từ 1 đến 4 và từ -1 đến 4 rồi so sánh \(f\left( { - 1} \right),f\left( 1 \right),f\left( 4 \right)\).
Lời giải
Ta thấy \(f'\left( x \right) = 0\) cắt đường thẳng \(Ox\) tại 3 điểm phân biệt.
Khi đó hàm số \(y = f\left( x \right)\) có ba cực trị \( \Rightarrow \) Khẳng định đúng \( \Rightarrow \) Loại.
Trên khoảng \(\left( {1; + \infty } \right)\) thì hàm số \(y = f\left( x \right)\) không đồng biến \( \Rightarrow \) Khẳng định 2 sai \( \Rightarrow \) Thỏa mãn.
Tính tích phân: \(\int\limits_{ - 1}^1 {f'\left( x \right)dx = f\left( 1 \right) - f\left( { - 1} \right) > 0} \) vì \(f'\left( x \right) > 0\forall x \in \left( { - 1;1} \right)\).
\( \Rightarrow f\left( 1 \right) > f\left( { - 1} \right)\)
vì \(f'\left( x \right) < 0\forall x \in \left( {1;4} \right)\).
\( \Rightarrow f\left( 1 \right) > f\left( 4 \right)\)
do phần diện tích bên dưới lớn hơn.
\( \Rightarrow f\left( { - 1} \right) > f\left( 4 \right)\)
\( \Rightarrow f\left( 1 \right) > f\left( { - 1} \right) > f\left( 4 \right)\)
Khẳng định 3 sai \( \Rightarrow \) Thỏa mãn.
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;4} \right]\) bằng \(f\left( 4 \right)\) vì \(f\left( 1 \right) > f\left( { - 1} \right) > f\left( 4 \right)\).
\( \Rightarrow \) Khẳng định đúng \( \Rightarrow \) Loại.
Chọn B, C
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp giải
Dựa vào nhiệt độ sôi của nước và etanol, chất nào bay hơi trước thì sẽ giảm nồng độ trước.
Lời giải
Khi chưng cất rượu nấu, etanol có nhiệt độ sôi thấp hơn nước sẽ bay hơi trước nên tỉ lệ etanol/nước sẽ tăng dần. Vậy nhận định trên là nhận định sai.
Chọn B
Lời giải
Phương pháp giải
Lời giải
Để \(\widehat {\vec u,\vec v)} < {90^ \circ } \Rightarrow {\rm{cos}}\widehat {\left( {\vec u,\vec v} \right)} > 0\).
\( \Rightarrow \vec u.\vec v > 0 \Leftrightarrow 3 + {\rm{lo}}{{\rm{g}}_3}5.{\rm{lo}}{{\rm{g}}_5}3 + 4{\rm{lo}}{{\rm{g}}_m}2 > 0\)
\( \Leftrightarrow 4 + 4{\rm{lo}}{{\rm{g}}_m}2 > 0 \Leftrightarrow {\rm{lo}}{{\rm{g}}_m}2 > - 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > 1}\\{m < \frac{1}{2}}\end{array}} \right.\).
Kết hợp điều kiện \(m > 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{m > 1}\\{0 < m < \frac{1}{2}}\end{array}} \right.\)
Chọn D
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận