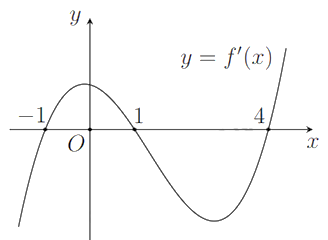Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 25)
57 người thi tuần này 4.6 1.1 K lượt thi 100 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 15)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 14)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 13)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 12)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 11)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 10)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 9)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 8)
Danh sách câu hỏi:
Đoạn văn 1
Đọc thông tin dưới đây và trả lời các câu hỏi từ câu 1 - câu 10:
LIÊN KẾT ĐA MÔ THỨC: MÙI HƯƠNG VÀ MÀU SẮC
[1] Năm giác quan của chúng ta thu thập thông tin ở mọi thời khắc. Con đường để não bộ của chúng ta cảm nhận được vô số thông tin là qua sự kết hợp thông tin từ hai hay nhiều giác quan khác nhau, như giữa các mùi và bề mặt trơn mượt của kết cấu, của độ cao thấp, màu sắc và các chiều kích âm nhạc.
[2] Có thể đó là nguyên nhân giải thích tại sao chúng ta bắt đầu liên kết các mức nhiệt cao hơn với những màu sắc ấm, các mức âm thanh thấp hơn với những vị trí ít được đánh giá, hoặc màu sắc với hương vị cụ thể của các món ăn. Một nghiên cứu mới lập luận rằng có rất nhiều mối liên quan “đa mô thức” mà ta không ý thức được với cảm nhận của chúng ta về mùi có thể ảnh hưởng đến nhận thức của chúng ta về màu sắc.
[3] Tác giả thứ nhất của tiến sĩ Ryan Ward, một giảng viên chính tại trường đại học Liverpool John Moores, và đồng nghiệp đã kiểm tra sự tồn tại và sức mạnh trong những liên kết mùi – màu sắc ở 24 người phụ nữ và đàn ông trưởng thành ở độ tuổi từ 20 đến 57. Những người tham gia ngồi trước một màn hình trong một căn phòng trống rỗng để tránh những kích thích lên giác quan không mong muốn trong suốt thời gian diễn ra thí nghiệm. Họ không dùng chất khử mùi hoặc nước hoa và không ai trong số những người này mắc bệnh mù màu hoặc liên quan đến nhận thức mùi.
[4] Tất cả các mùi xung quanh trong phòng bị cô lập đều được thanh lọc với một bộ lọc không khí trong vòng bốn phút. Sau đó một trong số bốn mùi (được chọn một cách ngẫu nhiên từ caramel, quả anh đào, cà phê, chanh vàng và bạc hà, cộng thêm nước không mùi như một chất kiểm soát) đã được đưa vào phòng với một thiết bị khuếch tán siêu thanh trong vòng năm phút.
[5] “Trong một nghiên cứu trước, chúng tôi đã chứng tỏ là mùi caramel nhìn chung tạo thành một liên kết đa phương thức với màu nâu tối và vàng, giống như cà phê với nâu tối và đỏ, quả anh đào với hồng, đỏ và tía, bạc hà với xanh lá cây và xanh lam, và chanh tây với vàng, xanh lá cây và hồng”, Ward giải thích.
[6] Những người tham gia đã được xem một màn hình, trên đó có một hình vuông mang màu sắc ngẫu nhiên (với một phạm vi hữu hạn), và được mời chọn một trong hai – vàng hay xanh lam, xanh lá cây hoặc đỏ – để thay đổi màu sắc cho ô xám trung tính. Sau khi ghi nhận quyết định cuối cùng, quá trình lại được lặp lại cho đến khi tất cả các mùi hương được xuất hiện năm lần.
[7] Kết quả cho thấy những người tham gia có một xu hướng yếu ớt nhưng đáng kể chấp thuận một trong hai màu khác màu xám trung tính. Ví dụ, khi hiển thị mùi của cà phê, họ thường có xu hướng nhận ‘màu xám’ thành màu đỏ nâu hơn là màu xám trung tính. Tương tự, khi hiện diện mùi caramel, họ thường nhận lầm màu xanh lam thành màu xám. Sự hiện diện của mùi thậm chí làm biến dạng nhận thức mùi của người tham gia theo một cách có thể dự đoán được.
[8] Duy chỉ có ngoại lệ khi mùi bạc hà tỏa ra: sự lựa chọn màu sắc của người tham gia khác biệt từ mối liên hệ đa mô thức điển hình liên kết với mùi khác. Và đúng như dự đoán, sự lựa chọn của người tham gia tương ứng với màu xám thực sự khi đi kèm với nước không mùi. “Các kết quả này chứng tỏ ý thức về màu xám có xu hướng tương ứng với những phản hồi đa mô thức dành cho bốn trong số năm mùi là chanh vàng, caramel, anh đào và cà phê”, Ward nói. “Sự bù quá mức này cho thấy vai trò của những liên kết đa mô thức trong xử lý thông tin đầu vào đủ ảnh hưởng lên cách chúng ta đón nhận thông tin từ các mùi khác nhau, ở đây là giữa mùi hương và màu sắc”.
[9] Điều này có thực sự đúng không? Điều này vẫn chưa được rõ cũng như là đa mô thức liên kết giữa mùi và màu sắc như thế nào. “Chúng ta cần biết mức độ mùi ảnh hưởng đến ý thức về mùi như thế nào. Ví dụ, sự ảnh hưởng vẫn hiện diện với những mùi ít gặp hay thậm chí là với cả mùi lần đầu tiên bắt gặp?”, Ward nói.
(Thanh Đức, Tạp chí Tia sáng, 03/12/2023, tiasang.com.vn)
Lời giải
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ đoạn [2]: “Có thể đó là nguyên nhân giải thích tại sao chúng ta bắt đầu liên kết các mức nhiệt cao hơn với những màu sắc ấm”.
=>Thông tin Đúng.
Chọn A
Lời giải
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [3], nói rõ rằng những người tham gia không sử dụng chất khử mùi hoặc nước hoa và không có ai trong số họ mắc bệnh mù màu hoặc vấn đề liên quan đến nhận thức mùi.
=> Thông tin Đúng.
Chọn A
Lời giải
Đáp án
Nghiên cứu của tiến sĩ Ryan Ward và các cộng sự về mối liên quan giữa mùi hương và màu sắc mang đến kết quả đầy thú vị về sự tương tác phức tạp giữa các giác quan của chúng ta. Ryan cho rằng mỗi mùi hương có thể kích thích sự thay đổi trong lựa chọn màu sắc của chúng ta, khẳng định giác quan của con người là một hệ thống liên kết, không chỉ hoạt động độc lập mà còn tương tác mạnh mẽ với nhau.
Phương pháp giải
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Lời giải
- [Vị trí thả 1]: cộng sự -> trong ngữ cảnh câu văn, “cộng sự” là những người hỗ trợ hoặc đồng nghiệp cùng thực hiện nghiên cứu với tiến sĩ Ryan Ward.
- [Vị trí thả 2]: kích thích -> trong ngữ cảnh câu văn và nội dung bài đọc, mùi hương có thể tác động đến sự lựa chọn màu sắc, nghĩa là “kích thích” sự thay đổi trong lựa chọn màu sắc.
- [Vị trí thả 3]: liên kết -> mối liên hệ, kết nối giữa các bộ phận trong cơ thể, có thể hoạt động độc lập và tác động lẫn nhau.
Câu 4
A. Mùi caramel thường được liên kết với màu đỏ và xanh lam.
B. Mùi cà phê chỉ ảnh hưởng đến màu sắc nâu đậm.
C. Mùi bạc hà không tạo ra liên kết đa mô thức.
Lời giải
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
- C đúng - Căn cứ nội dung đoạn [8]: “Duy chỉ có ngoại lệ khi mùi bạc hà tỏa ra: sự lựa chọn màu sắc của người tham gia khác biệt từ mối liên hệ đa mô thức điển hình liên kết với mùi khác.” -> mùi bạc hà không tạo ra liên kết đa mô thức.
- A sai - Căn cứ nội dung đoạn [5]: “chúng tôi đã chứng tỏ là mùi caramel nhìn chung tạo thành một liên kết đa phương thức với màu nâu tối và vàng”.
- B sai - Căn cứ nội dung đoạn [5]: “giống như cà phê với nâu tối và đỏ”.
- D sai - Căn cứ nội dung đoạn [9]: “những liên kết đa mô thức trong xử lý thông tin đầu vào đủ ảnh hưởng lên cách chúng ta đón nhận thông tin từ các mùi khác nhau, ở đây là giữa mùi hương và màu sắc” -> sự lựa chọn màu sắc có ảnh hưởng bởi mùi hương.
=> Đáp án cần chọn là C.
Lời giải
Đáp án: "Xu hướng"
Phương pháp giải
Xét logic câu từ và thông tin có được sau bài đọc.
Lời giải
Trong ngữ cảnh câu văn, thị trường công nghệ đang chuyển dịch là một “xu hướng” -> “xu hướng” xuất hiện trong đoạn [7] và [8] của bài đọc.
=> Từ cần điền là Xu hướng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. Đối chiếu mức độ ảnh hưởng của mùi đối với màu sắc.
B. Xác định mối liên quan giữa mùi và âm thanh.
C. Chứng minh rằng mỗi người có cùng một trải nghiệm với mùi và màu sắc.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. Từ 9 đến 29 tuổi
B. Từ 19 đến 39 tuổi
C. Từ 29 đến 49 tuổi
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc thông tin dưới đây và trả lời các câu hỏi từ câu 11 - câu 20:
DI SẢN PHẬT GIÁO CHÙA THIÊN MỤ
[1] Huế là miền đất Phật giáo. Nơi đây có nhiều chùa chiền, thiền viện gắn với lịch sử phát triển Phật giáo xứ Đàng Trong thời chúa Nguyễn đi mở cõi và miền Trung sau này. Trong số đó, ngôi cổ tự nổi tiếng nhất là chùa Thiên Mụ, được mệnh danh là đệ nhất danh lam xứ Huế.
[2] Chùa Thiên Mụ (hay còn gọi là chùa Linh Mụ) nằm trên đồi Hà Khê, tả ngạn sông Hương, cách Kinh thành Huế chừng 5km về hướng Tây, xưa thuộc địa phận huyện Hương Trà (nay là phường Hương Long, thành phố Huế). Chùa Thiên Mụ chính thức khởi lập năm 1601, được coi là dấu ấn gắn liền với bước chân mở cõi của Tiên chúa Nguyễn Hoàng, đặt nền móng cho Phật giáo của người Việt ở xứ Đàng Trong.
[3] Chùa Thiên Mụ gắn liền với một truyền thuyết lâu đời. Chuyện kể rằng, từ xa xưa, dân chúng nơi này đêm đêm thường thấy một bà già mặc áo đỏ, quần lục xuất hiện trên ngọn đồi mà chùa tọa lạc ngày nay, nói rằng: Rồi sẽ có một vị chân chúa đến lập chùa ở đây để tụ long khí, làm bền long mạch cho nước Nam hùng mạnh. Nói xong, bà biến mất. Từ đó, ngọn đồi đặt tên là Thiên Mụ Sơn (núi Bà Trời). Sau khi vào trấn thủ Thuận Hóa, chúa Nguyễn Hoàng (1558 - 1613) một lần đi qua đây đã nghe được câu chuyện ấy. Chúa Nguyễn Hoàng cho rằng đó là điềm ứng với mình. Năm 1601, chúa cho xây dựng một ngôi chùa trên đồi, nhìn thẳng ra sông Hương và đặt tên là “Thiên Mụ”.
[4] Trước đó, trên đồi Hà Khê đã có một ngôi chùa của người Chăm, tên là Thiên Mỗ (hoặc Thiên Mẫu). Nhưng có lẽ thời đó chùa còn đơn sơ nhỏ hẹp nên vào năm 1601, chúa Nguyễn Hoàng đã cho xây dựng lại với quy mô lớn hơn. Năm 1665, dưới thời chúa Nguyễn Phúc Tần, chùa được trùng tu. Dưới thời chúa Nguyễn Phúc Chu (1691 - 1725), theo đà phát triển và hưng thịnh của Phật giáo xứ Đàng Trong, chùa được xây dựng lại với quy mô lớn hơn. Năm 1710, chúa Nguyễn Phúc Chu cho đúc Đại hồng chung và khắc một bài minh lên chuông. Năm 1714 lại cho trùng tu và mở rộng chùa, xây thêm nhiều công trình trong quần thể. Khi hoàn thành, chúa lại viết một bài ký và cho khắc vào bia đá để kỷ niệm. Dưới thời Tây Sơn, chùa bị binh hỏa tàn phá nặng nề. Chùa được trùng tu vào năm 1815 và 1831 dưới thời vua Gia Long và vua Minh Mạng nhà Nguyễn. Năm 1844, vua Thiệu Trị lại cho trùng tu, xây thêm tháp Phước Duyên và đình Hương Nguyện, dựng hai tấm bia đá ghi khắc thơ văn của nhà vua.
[5] Thiên Mụ là ngôi chùa cổ nhất xứ Huế và xứ Đàng Trong. Kiến trúc của ngôi chùa được lồng ghép vào cảnh thiên nhiên nên thơ, tĩnh mịch. Cảnh quan của ngôi chùa rất đặc biệt, không nơi nào có được. Ngọn đồi đột khởi giữa khoảng đất bằng được nhấn mạnh bởi ngọn tháp Phước Duyên làm cho khung cảnh thêm uy nghi. Dòng sông Hương trong xanh uốn khúc trước chùa khiến phong cảnh nơi đây thêm hữu tình.
[6] Thời cực thịnh, trong chùa có tới vài chục công trình. Trải qua nhiều biến động, hiện chùa Thiên Mụ có khuôn viên rộng 100m x 280m với các hạng mục: Tứ trụ, tháp Phước Duyên, 2 nhà bia thời Thiệu Trị, đại hồng chung; các bia đá thời chúa Nguyễn Phúc Chu, Thành Thái, Khải Định; tam quan, lầu chuông, lầu trống, điện Quan Âm, nhà tăng... Cuối quần thể là mộ phần hòa thượng Thích Đôn Hậu - người từng trụ trì chùa Thiên Mụ trong thời gian dài và có nhiều đóng góp cho Phật giáo Việt Nam.
[7] Trong số các hạng mục kiến trúc, tiêu biểu nhất là tháp Phước Duyên. Tháp có mặt bằng hình bát giác, cao 7 tầng (21m), dáng thuôn dần từ đế lên đỉnh. Trong tháp có hệ thống bậc thang xây cuốn lên tầng 6, từ tầng 6 lên tầng 7 dùng thang gỗ. Mỗi tầng tháp đều có tượng Phật. Ở tầng trên cùng xưa có tượng Phật bằng vàng, nay không còn nữa.
[8] Tháp Phước Duyên là một kiến trúc đậm dấu ấn mỹ thuật Phật giáo, là một trong những biểu tượng của cố đô. Công trình tiêu biểu tiếp theo là điện Đại Hùng - điện thờ chính và là nơi hành lễ. Đây là một ngôi điện lớn với kiểu kiến trúc “trùng thiềm điệp ốc”. Trong lần trùng tu năm 1957, nhiều cấu kiện gỗ đã được thay bằng bê tông. Tuy nhiên, cấu trúc ngôi điện vẫn được giữ nguyên. Tại gian giữa tiền điện có treo bức hoành phi bằng gỗ sơn son thếp vàng do chúa Nguyễn Phúc Chu ngự đề năm 1714.
[9] Trong số các di vật, pháp khí được lưu giữ ở chùa thì tiêu biểu nhất là đại hồng chuông do chúa Nguyễn Phúc Chu cho đúc năm 1710. Chuông có kích thước cao 2,5m, đường kính 1,4m, nặng 2.052kg, được coi là tác phẩm điêu khắc đồng nghệ thuật xuất sắc của Việt Nam ở thế kỷ XVIII. Mặt trên của chuông chia làm 4 khoảng, khắc bài minh của chúa Nguyễn Phúc Chu và chạm nổi những hình long, vân, nhật, tinh; phần dưới khắc hình bát quái và thủy ba. Đại hồng chung chùa Thiên Mụ đã được công nhận là Bảo vật quốc gia năm 2013.
[10] Chùa Thiên Mụ là một di sản Phật giáo quý của Việt Nam. Với kiến trúc uy nghiêm cổ kính, cảnh trí nên thơ, chùa Thiên Mụ xứng danh là "đệ nhất danh lam xứ Huế".
(Hà Thành, Báo Hà Nội Mới, 04/09/2023, hanoimoi.vn)
Câu 11
A. Thiên Mụ - Ngôi cổ tự nổi tiếng của Huế
B. Phật giáo ở Đàng Trong và dấu ấn của chùa Thiên Mụ
C. Lịch sử và kiến trúc của chùa Thiên Mụ
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. Chùa Thiên Mụ được xây dựng vào năm 1601 và đặt tên theo truyền thuyết về bà già mặc áo đỏ.
B. Truyền thuyết về bà già xuất hiện trên ngọn đồi của chùa Thiên Mụ kể về việc có một vị chân chúa đến lập chùa để tụ long khí cho nước Nam.
C. Chùa Thiên Mụ được coi là “Đệ nhất danh lam xứ Huế” nhờ vào truyền thuyết về bà già áo đỏ và dự đoán về sự hùng mạnh của nước Nam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. Chùa Thiên Mụ được xây dựng lần đầu vào thế kỷ 17, sau khi chúa Nguyễn Hoàng nghe về truyền thuyết của bà già áo đỏ.
B. Vua Thiệu Trị cho trùng tu chùa Thiên Mụ và xây thêm tháp Phước Duyên và bia khắc thơ văn nhà vua.
C. Chùa Thiên Mụ đã bị tàn phá nặng nề bởi binh hỏa trong thời kỳ Tây Sơn, nhưng sau đó được trùng tu và phục hồi dưới thời vua Gia Long.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc thông tin dưới đây và trả lời các câu hỏi từ câu 21 - câu 27:
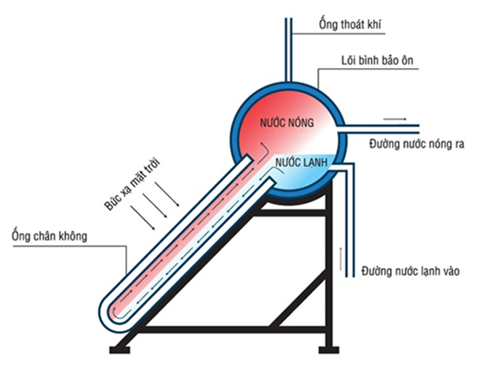
Sử dụng năng lượng tái tạo đang là một xu hướng của các quốc gia đang hướng tới để có thể giải quyết các vấn đề về môi trường. Một trong số đó có thể kể đến là nguồn năng lượng mặt trời. Ở những nơi có nguồn ánh nắng dồi dào, máy nước nóng năng lượng mặt trời là thiết bị thường được sử dụng. Thiết bị này thường được đặt trên tầng thượng

Ống hấp thụ nhiệt là bộ phận hết sức quan trọng của một máy nước nóng năng lượng mặt trời, gồm có hai lớp với khả năng chịu được va đập cao và ở giữa là lớp chân không. Tác dụng của bộ phận này là hấp thụ và truyền nhiệt để làm nóng nước. Một trong số các loại máy nước nóng phổ biến hiện nay là máy nước nóng năng lượng mặt trời sử dụng ống chân không. Chi tiết cấu tạo được thể hiện trong hình sau:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A. 4200J
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc thông tin dưới đây và trả lời các câu hỏi từ câu 28 - câu 34:
Nhu cầu sử dụng điện của các hộ gia đình hiện nay ngày càng tăng cao. Mọi hoạt động sinh hoạt hằng ngày phần lớn đều cần dùng đến điện.
Tuy nhiên, vì tính chất của điện và để đảm bảo sự an toàn cho mọi người, máy phát điện không thể để gần các hộ gia đình. Do đó, để truyền tải điện năng đi xa để đáp ứng nhu cầu sử dụng của mọi nhà. Cũng như khi truyền tải điện năng đi xa, để giảm hao phí điện năng tốt hơn.
Đồng thời khi cần phải truyền tải điện năng đi xa sẽ bằng các đường dây truyền tải điện. Người ta không sử dụng dòng điện 1 chiều mà sẽ sử dụng dòng điện xoay chiều cho các máy biến thế. Nguyên nhân vì quy trình hoạt động của máy biến thế dựa trên hiện tượng cảm ứng điện từ. Điều này cho thấy muốn có hiện tượng cảm ứng điện từ thì từ thông qua cuộn dây phải biến thiên. Vì vậy, chỉ có dòng điện xoay chiều mới làm cho từ thông biến thiên.
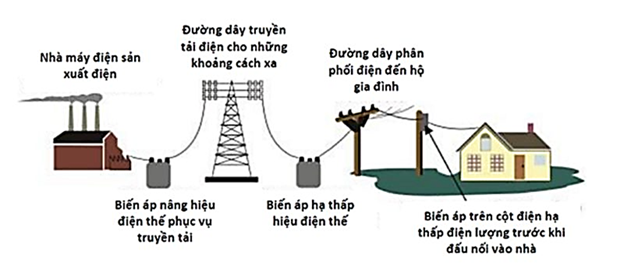
Trong quá trình truyền tải điện năng đi xa bằng dây dẫn, có một phần điện năng bị hao phí. Nguyên nhân là vì xuất hiện hiện tượng tỏa nhiệt trên đường dây. Với mô hình truyền tải lí tưởng khi nâng điện áp tại nguồn lên k lần thì công suất hao phí giảm đi k2. Gọi R là điện trở đường dây, P là công suất truyền đi, U là điện áp nơi phát, cosφ là hệ số công suất của mạch thì công suất hao phí trên dây là: \(\Delta P = R{I^2} = R\frac{{{P^2}}}{{{{(U\cos \varphi )}^2}}}\)
Hiệu suất truyền tải được xác định bằng: \(H = \frac{{P - \Delta P}}{P}.100\% \)
Cách để giảm hao phí trên đường dây tải điện là giảm điện trở R của đường dây hoặc tăng hiệu điện thế hai đầu dây dẫn. Dòng điện xoay chiều có khả năng truyền tải ở cự li xa với hao phí thấp hơn với cách tăng hiệu điện thế hai đầu đây dẫn. Cách tăng hiện điện thế ở hai đầu dây dẫn được coi là cách tối ưu và hiệu quả nhất, được áp dụng nhiều trong thực tế. Cách làm đó được thực hiện bằng máy biến áp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. giảm 1,44 lần
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
A. Tăng cường độ của dòng điện không đổi.
B. Giảm điện áp của dòng điện xoay chiều.
C. Giảm hao phí trong truyền tải điện năng đi xa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
A. 1736 kW.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Đọc thông tin dưới đây và trả lời các câu hỏi từ câu 35 - câu 41:
PHƯƠNG PHÁP CHƯNG CẤT HỢP CHẤT HỮU CƠ
Các hợp chất hữu cơ thu được trong tự nhiên hay bằng con đường tổng hợp trong phòng thí nghiệm thường ở dạng thô, lẫn các tạp chất cần phải loại bỏ. Muốn có được sản phẩm hữu cơ tinh khiết người ta thường sử dụng các phương pháp nhằm tách biệt và tinh chế các hợp chất hữu cơ.
Phương pháp chưng cất là một phương pháp nhằm tách biệt và tinh chế hợp chất hữu cơ rất phổ biến. Chưng cất là phương pháp tách chất dựa vào sự khác nhau về nhiệt độ sôi của các chất trong hỗn hợp ở một áp suất nhất định. Người ta chuyển chất lỏng cần tách sang pha hơi, rồi làn lạnh cho hơi ngưng tụ, thu lấy chất lỏng ở khoảng nhiệt độ thích hợp. Phương pháp chưng cất dùng để tách các chất lỏng ra khỏi hỗn hợp các chất có nhiệt độ sôi khác nhau nhằm thu được chất lỏng tinh khiết hơn.
Có ba kiểu chưng cất phổ biến trong công nghiệp và đời sống. Phương pháp chưng cất phân đoạn dùng để tách hai hay nhiều chất lỏng có nhiệt độ sôi khác nhau không nhiều và tan lẫn hoàn toàn trong nhau. Thiết bị và dụng cụ của phương pháp chưng cất phân đoạn được bố trí như hình dưới đây:
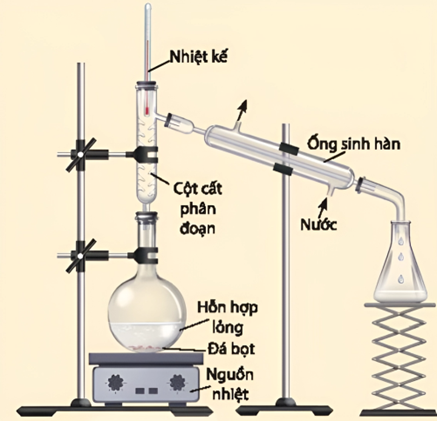
Hình 1. Sơ đồ thiết bị chưng cất phân đoạn
Trong thực tế, việc chưung cất được tiến hành thuận lợi khi chất lỏng có nhiệt độ sôi khoảng 40oC đến 150oC, vì trên 150oC nhiều chất lỏng bị phân huỷ; ngược lại hơi của chất lỏng có nhiệt độ sôi thấp sẽ khó ngưng tụ và sản phẩm bị thất thoát nhiều khi chưng cất thông thường. Để chưng cất được những chất lỏng có nhiệt độ sôi cao, người ta có thể tiến hành chưng cất lôi cuốn hơi nước để hạn chế sự phân huỷ của chất. Phương pháp chưng cất lôi cuốn hơi nước được áp dụng để chưng cất chất lỏng có nhiệt độ sôi cao và không tan trong nước. Trong phương pháp chưng cất lôi cuốn hơi nước, các chất có nhiệt độ sôi cao và không tan trong nước vẫn có thể tách ra khỏi hỗn hợp ở nhiệt độ sôi xấp xỉ nhiệt đôi sôi của nước. Thiết bị chưng cất lôi cuốn hơi nước được bố trí như hình 2. Hỗn hợp hơi nước và hơi chất hữu cơ cùng đi qua ống sinh hàn ngưng tụ và được thu ở bình hứng:
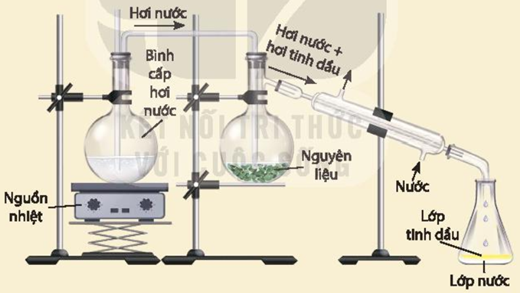
Hình 2. Sơ đồ thiết bị chưng cất lôi cuốn hơi nước
Nấu rượu gạo truyền thống là một phương pháp nấu rượu hoàn toàn thủ công, đòi hỏi người nấu phải có kinh nghiệm và tuân thủ đúng quy trình chưng cất mới sản xuất được rượu đạt chuẩn. Sau giai đoạn ủ men rượu, người ta thu được một hỗn hợp chủ yếu gồm nước (nhiệt độ sôi là 100oC), rượu etylic (C2H5OH) (nhiệt độ sôi là 78,3oC), axit axetic (nhiệt độ sôi là 117,9oC),... và bã rượu. Chưng cất hỗn hợp này, đầu tiên sẽ thu được một dung dịch chứa nhiều ethanol hơn trước, sau đó hàm lượng ethanol giàm dần.
Các bạn học sinh tiến hành thí nghiệm chưng cất etanol từ rượu được nấu thủ công như sau:
Bước 1: Cho 60 mL rượu được nấu thủ công vào bình cầu có nhánh (chú ý chất lỏng trong bình không vượt quá 2/3 thể tích bình), thêm vài viên đá bọt.
Bước 2: Lắp bộ dụng cụ như hình dưới đây:

Bước 3: Đun nóng hỗn hợp từ từ đến khi hỗn hợp sôi, quan sát nhiệt độ trên nhiệt kế thấy tăng dần, khi nhiệt độ trên nhiệt kế ổn định, đó chính là nhiệt độ sôi của hỗn hợp etanol và nướC. Khi nhiệt độ bắt đầu tăng trở lại, ngừng chưng cất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
A. Phương pháp chưng cất phân đoạn.
B. Phương pháp chưng cất lôi cuốn hơi nước.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 41
A. sản xuất muối tinh từ cánh đồng muối.
B. ngâm rượu.
C. sản xuất tinh dầu cam chanh từ vỏ chanh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 6
Đọc thông tin dưới đây và trả lời các câu hỏi từ câu 42 - câu 48:
CHẤT XÚC TÁC TRONG PHẢN ỨNG HOÁ HỌC
Các yếu tố làm tăng tốc độ phản ứng bao gồm nồng độ (đối với dung dịch), áp suất (đối với chất khí), nhiệt độ, diện tích tiếp xúc của các chất và chất xúc tác. Trong đó, chất xúc tác là yếu tố khác với các yếu tố còn lại. Khi tăng 4 yếu tố còn lại thì tốc độ phản ứng tăng còn đối với chất xúc tác thì sự có mặt của nó làm cho tốc độ phản ứng tăng mà khối lượng và bản chất của nó không bị thay đổi sau khi phản ứng kết thúc.
Chất xúc tác có thể được chia thành hai nhóm chính: chất xúc tác đồng thể và chất xúc tác dị thể. Trong một phản ứng dị thể, chất xúc tác ở một pha khác (rắn, lỏng hoặc khí) so với các chất phản ứng. Trong một phản ứng đồng thể, chất xúc tác ở cùng pha với các chất phản ứng. Các xúc tác dị thể đều trải qua giai đoạn giống nhau.
Học sinh làm thí nghiệm chuyển hoá propanol thành propen sử dụng xúc tác là bột nhôm, sau đó tiếp tục chuyển hoá propen thành propanol với xúc tác là paladi.
Thí nghiệm 1:
Hai ống tiêm thủy tinh được nối với ống xúc tác có chứa bột nhôm (Hình 1). Ống tiêm có thể tích 1 ml chứa đầy 1 ml propanol. tiếp theo, thiết bị được giữ trên ngọn lửa của đèn đốt và ống xúc tác bột nhôm được làm nóng nhẹ trong khi propanol lỏng được đưa từ từ vào ống xúc tác. Chất lỏng chảy qua ống cho đến khi chạm vào vùng nóng. sau đó nó bay hơi, phản ứng với chất xúc tác và thoát ra khỏi ống xúc tác dưới dạng khí propen vào ống tiêm thu khí có thể tích là 60 ml. quy trình được lặp lại với lượng propanol và bột nhôm khác nhau và lượng propen dạng khí thu được được ghi lại (Bảng 1).

(C2H5OH) (nhiệt độ sôi là 78,3)
Hình 1: Mô hình thí nghiệm 1
Bảng 1. Kết quả của thí nghiệm 1
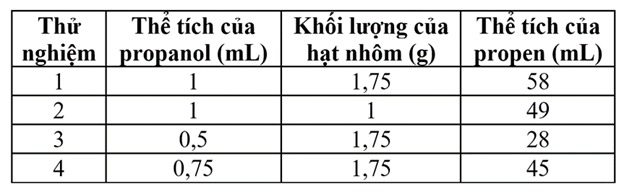
Thí nghiệm 2:
Một ống tiêm chất phản ứng chứa đầy thể tích hiđro và propen bằng nhau. Ống tiêm chất phản ứng và ống tiêm thu sản phẩm được nối với ống xúc tác chứa đầy paladi rắn như trong hình 2. Sau đó hỗn hợp hiđro-propen được truyền từ từ qua chất xúc tác, phản ứng xảy ra và propan được thu vào ống tiêm thu. Quy trình được lặp lại nhiều lần, thay đổi khoảng thời gian chất phản ứng được truyền qua chất xúc tác. Kết quả được thể hiện ở bảng 2.

Hình 2. Mô hình thí nghiệm 2
Bảng 2. Kết quả thực hiện thí nghiệm 2
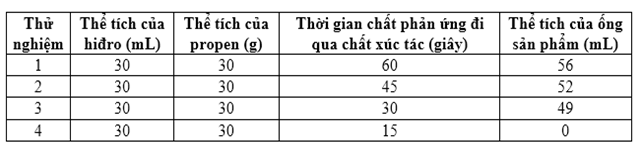
Câu 42
A. giảm chậm trong 30 giây.
B. tăng ngay lập tức, sau đó giảm dần khi phản ứng xảy ra.
C. giữ nguyên cho đến khi xảy ra phản ứng rồi giảm dần.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 48
A. không có đủ thể tích hiđro và propen để tạo ra phản ứng.
B. 15 giây là khoảng thời gian quá dài để chất phản ứng truyền qua chất xúc tác.
C. không có đủ thể tích palladium trong ống xúc tác để tạo ra phản ứng và tạo ra propan.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 7
Đọc thông tin dưới đây và trả lời các câu hỏi từ câu 49 - câu 51:
Tế bào - đơn vị cấu trúc và chức năng cơ bản của mọi sinh vật—có hai loại riêng biệt: sinh vật nhân sơ và sinh vật nhân chuẩn. Vi khuẩn và Archaea (vi khuẩn cổ) có cấu trúc tế bào là tế bào nhân sơ. Sinh vật nguyên sinh, nấm, động vật và thực vật đều được cấu tạo từ tế bào nhân chuẩn.
Tất cả các tế bào đều có chung một số đặc điểm cơ bản nhất định: chúng đều được bao bọc bởi một màng chọn lọc, được gọi là màng sinh chất (còn gọi là màng tế bào). Bên trong tất cả các tế bào là một chất bán lỏng, giống như thạch gọi là bào tương, trong đó các thành phần dưới tế bào được cấm. Tất cả các tế bào đều chứa nhiễm sắc thể, mang gen ở dạng DNA và ribosome, những phức hợp nhỏ tạo ra protein.
Sự khác biệt chính giữa tế bào nhân sơ và tế bào nhân chuẩn là vị trí DNA của chúng. Ở tế bào nhân chuẩn, hầu hết DNA nằm trong một cơ quan gọi là nhân, được bao bọc bởi một màng kép. Ở tế bào nhân sơ, DNA tập trung ở một vùng không có màng bao bọc, gọi là nucleoid (vùng nhân).
Câu 49
A. Vi khuẩn.
B. Archaea (vi khuẩn cổ).
C. Sinh vật nguyên sinh.
D. Thực vật.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 8
Đọc thông tin dưới đây và trả lời các câu hỏi từ câu 52 - câu 57:
Thalassemia (còn được gọi là bệnh tan máu bẩm sinh), là một bệnh lý huyết học di truyền liên quan đến sự bất thường của hemoglobin (một cấu trúc protein trong hồng cầu có chức năng vận chuyển oxy). Ở bệnh nhân Thalassemia, các hồng cầu bị phá hủy quá mức dẫn đến tình trạng thiếu máu.
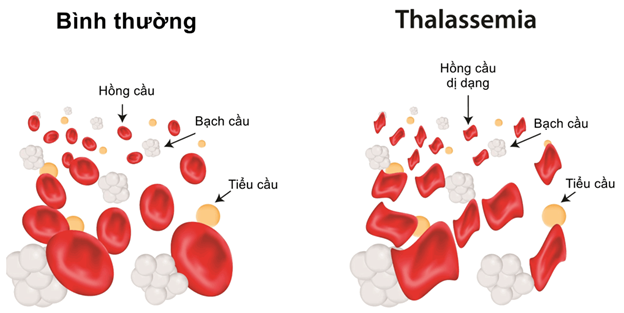
Thalassemia là một bệnh di truyền lặn trên nhiễm sắc thể thường. Tỷ lệ người mang gen bệnh là khoảng 7% dân số thế giới, trong đó có khoảng 1.1% cặp vợ chồng có nguy cơ sinh con bị bệnh hoặc mang gen bệnh Thalassemia, ước tính mỗi năm có khoảng 300.000 đến 500.000 trẻ sinh ra mắc Thalassemia ở mức độ nặng. Tại Việt Nam, bệnh Thalassemia được ghi nhận từ năm 1960, hiện nay có khoảng 10 triệu người mang gen bệnh, khoảng 20000 người bị Thalassemia thể nặng, ước tính mỗi năm có khoảng 2000 trẻ sinh ra mắc bệnh Thalassemia.
Hemoglobin gồm có 2 thành phần là Hem và globin, trong globin gồm có các chuỗi polypeptid. Bệnh Thalassemia xảy ra khi có đột biến tại một hay nhiều gen liên quan đến sự tổng hợp các chuỗi globin, dẫn đến tình trạng thiếu hụt các chuỗi globin này, làm cho hồng cầu vỡ sớm (tan máu), và biểu hiện triệu chứng thiếu máu. Bệnh nhân mắc Thalassemia có thể nhận gen bệnh từ bố hoặc mẹ, hoặc cả bố và mẹ.
Bệnh được gọi tên theo chuỗi globin bị khiếm khuyết, gồm có 2 loại bệnh Thalassemia chính:
+ α-Thalassemia: Thiếu hụt tổng hợp chuỗi α, do đột biến tại một hay nhiều gen tổng hợp chuỗi α-globin.
+ β-Thalassemia: Thiếu hụt tổng hợp chuỗi β, do đột biến tại một hay nhiều gen tổng hợp chuỗi β-globin.
Câu 52
A. Bệnh di truyền gen lặn trên NST giới tính X.
B. Bệnh di truyền gen lặn trên NST giới tính Y.
C. Bệnh di truyền gen lặn trên NST thường.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 9
Đọc thông tin dưới đây và trả lời các câu hỏi từ câu 38 - câu 40:
Nuôi cấy mô In Vitro là thuật ngữ dùng để chỉ quá trình nuôi cấy vô trùng trong ống nghiệm các bộ phận tách rời khác nhau của thực vật. Kỹ thuật nuôi cấy mô In vitro dùng cho cả hai mục đích nhân giống và cải thiện di truyền (ví dụ: giống cây trồng), sản xuất sinh khối các sản phẩm hóa sinh, bệnh học thực vật, duy trì và bảo quản các nguồn gen quý…
Các hình thức nuôi cấy mô gồm có nuôi cấy mô thực vật và nuôi cấy mô bằng tế bào trần:
- Nuôi cây mô tế bào trần:
Tế bào trần thực chất là tế bào đơn được tách lớp vỏ cellulose, có sức sống và duy trì đầy đủ các chức năng sẵn có. Tế bào trần có thể tách trực tiếp từ các bộ phận của thực vật (lá, rễ) bằng cơ học. Trong điều kiện nuôi cấy thích hợp, tế bào trần có khả năng tái sinh màng tế bào, tiếp tục phân chia và tái sinh thành cây hoàn chỉnh. Hiện nay kỹ thuật nuôi cấy tế bào trần đang được nghiên cứu và hoàn thiện.
- Nuôi cấy mô thực vật:
Nuôi cấy mô tế bào thực vật là một lĩnh vực của công nghệ sinh học thực vật. Dựa trên tính toàn năng của tế bào và khả năng biệt hóa, phản biệt hóa của chúng mà người ta có thể tái sinh cây từ một tế bào hay một mẫu mô nào đó.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
A. Tế bào đã tách bỏ vỏ cellulose.
B. Tế bào chỉ được tách trực tiếp từ mô rễ.
C. Tế bào giữ chức năng tương tự như một tế bào bình thường.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
A. \(C_6^3\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
A. Nếu \(f'\left( x \right) \ge 0,\forall x \in \left( {a;b} \right)\) thì hàm số \(f\) đồng biến trên khoảng \(\left( {a;b} \right)\).
B. Điểm \({x_0}\) là điểm cực trị của hàm số \(f\) nếu \(f'\left( x \right)\) đổi dấu khi \(x\) đi qua \({x_0}\).
C. Hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) luôn đồng biến trên \(D = \left( { - \infty ; - 1} \right) \cup \left( { - 1; + \infty } \right)\).
D. Cho hàm số \(f\) có đạo hàm cấp hai trên khoảng \(\left( {a;b} \right)\). Nếu \({x_0} \in \left( {a;b} \right)\) thỏa mãn \(f'\left( {{x_0}} \right) = 0\) và \(f''\left( {{x_0}} \right) < 0\) thì \({x_0}\) là điểm cực đại của hàm số \(f\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
A. Hàm số \(y = f\left( x \right)\) có ba cực trị.
B. Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
C. Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
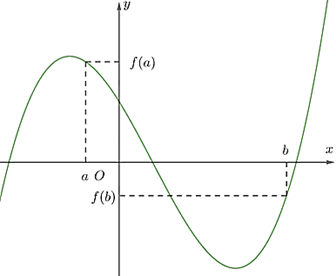
D. Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;4} \right]\) bằng \(f\left( 4 \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 76
A. 30
B. 101
C. 2070
D. 1980
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
A. Hàm số đã cho xác định với mọi \(x \in \mathbb{R}\).
B. Hàm số đã cho là hàm số chẵn.
D. Đồ thị của hàm số đã cho là một parabol.
E. Giới hạn \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } f\left( x \right) = + \infty ,\mathop {{\rm{lim}}}\limits_{x \to - \infty } f\left( x \right) = + \infty \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.