ĐGTD ĐH Bách khoa - Vấn đề thuộc lĩnh vực vật lí - Viết phương trình dao động điều hòa
41 người thi tuần này 4.6 1.7 K lượt thi 13 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội năm 2026 có đáp án (Đề 03)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội năm 2026 có đáp án (Đề 02)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội năm 2026 có đáp án (Đề 01)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 3)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 15)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 14)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 13)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 12)
Danh sách câu hỏi:
Câu 1
A. x = 5cos(2πt – π/2)(cm)
B. x = 5cos(2πt + π/2)(cm)
C. x = 5cos(πt – π/2)(cm)
D. x = 5cos(πt + π/2)(cm)
Lời giải
Trả lời:
Ta có:
A = 5 cm, T = 2s \[\omega = \frac{{2\pi }}{T} = \pi \,rad/s\]
Tại t = 0 \[\left\{ {\begin{array}{*{20}{c}}{x = 0}\\{v >0}\end{array}} \right. \leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\cos \varphi = 0}\\{\sin \varphi < o}\end{array}} \right. \to \varphi = - \frac{\pi }{2}\]
\[x = A\cos \left( {\omega t + \varphi } \right) = 5\cos \left( {\pi t - \frac{\pi }{2}} \right)cm\]
Đáp án cần chọn là: C
Câu 2
A. \[x = 16\cos \left( {2\pi t - \frac{\pi }{2}} \right)\left( {cm} \right)\]
B. \[x = 16\cos \left( {2\pi t + \frac{\pi }{2}} \right)\left( {cm} \right)\]
C. \[x = 8\cos \left( {2\pi t + \frac{\pi }{2}} \right)\left( {cm} \right)\]
D. \[x = 8\cos \left( {2\pi t - \frac{\pi }{2}} \right)\left( {cm} \right)\]
Lời giải
Trả lời:
Ta có:
A = 8cm
v = ωR = ωA = 16π
\[ \to \omega = \frac{{16\pi }}{8} = 2\pi \,\]
Mặt khác, tại thời điểm ban đầu, chất điểm đi qua tâm O =>x = 0, nằm trong mặt phẳng có quỹ đạo có chiều từ trái qua phải =>v >0
\[ \to \varphi = - \frac{\pi }{2}\]
\[ \to x = 8\cos \left( {2\pi t - \frac{\pi }{2}} \right)cm\]
Đáp án cần chọn là: D
Câu 3
A. \[x = 5\sqrt 2 \sin \left( {2\pi t + \frac{\pi }{4}} \right)cm\]
B. \[x = 5\cos \left( {2\pi t - \frac{\pi }{6}} \right)cm\]
C. \[x = 5\sin \left( {2\pi t + \frac{\pi }{4}} \right)cm\]
D. \[x = 5\sqrt 2 \sin \left( {2\pi t - \frac{\pi }{6}} \right)cm\]
Lời giải
Trả lời:
Ta có:
Tốc độ góc: ω = 2πf = 2π.1 = 2π(rad/s)
Biên độ dao động:
\[{A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {5^2} + {\left( {\frac{{10\pi }}{{2\pi }}} \right)^2}\]
\[ \Rightarrow A = 5\sqrt 2 cm\]
Tại t = 0:
\[\left\{ {\begin{array}{*{20}{c}}{x = A\cos \varphi = 5}\\{V = - A\omega \sin \varphi >0}\end{array}} \right. \to \left\{ {\begin{array}{*{20}{c}}{\cos \varphi = \frac{5}{{5\sqrt 2 }}}\\{\sin \varphi < 0}\end{array}} \right.\]
\[ \Rightarrow \varphi = - \frac{\pi }{4}\]
\[ \Rightarrow x = 5\sqrt 2 \cos \left( {2\pi t - \frac{\pi }{4}} \right)cm\]
\[ \Rightarrow x = 5\sqrt 2 \sin \left( {2\pi t - \frac{\pi }{4} + \frac{\pi }{2}} \right)\]
\[ \Rightarrow x = 5\sqrt 2 \sin \left( {2\pi t + \frac{\pi }{4}} \right)cm\]
Đáp án cần chọn là: A
Câu 4
A. \[x = 2\cos \left( {\pi t - \frac{\pi }{4}} \right)cm\]
B. \[x = 4\cos \left( {2\pi t - \frac{\pi }{2}} \right)cm\]
C. \[x = 2\cos \left( {\pi t + \frac{\pi }{2}} \right)cm\]
D. \[x = 4\cos \left( {\pi t - \frac{\pi }{2}} \right)cm\]
Lời giải
Trả lời:
Ta có: Thời gian vật đi từ VTCB đến A là :
\[\frac{T}{4} = 0,5 \to T = 2s\]
\[ \to \omega = \frac{{2\pi }}{T} = \pi \,rad/s\]
Biên độ A = 4cm
Tại t = 0: \[\left\{ {\begin{array}{*{20}{c}}{x = A\cos \varphi = 0}\\{v = - A\omega \sin \varphi >0}\end{array}} \right. \to \left\{ {\begin{array}{*{20}{c}}{\cos \varphi = 0}\\{\sin \varphi < 0}\end{array}} \right.\]
\[ \Rightarrow \varphi = - \frac{\pi }{2}\]
\[ \Rightarrow x = 4\cos \left( {\pi t - \frac{\pi }{2}} \right)cm\]
Đáp án cần chọn là: D
Câu 5
A. \[x = 4\cos \left( {\frac{\pi }{3}t - \frac{\pi }{3}} \right)cm\]
B. \[x = 4\cos \left( {\frac{\pi }{3}t + \frac{\pi }{6}} \right)cm\]
C. \[x = 4\cos \left( {\pi t - \frac{\pi }{6}} \right)cm\]
D. \[x = 4\cos \left( {\frac{{2\pi }}{3}t - \frac{{5\pi }}{6}} \right)cm\]
Lời giải
Trả lời:
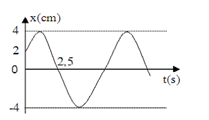
Từ đồ thị, ta có: A = 4cm
Thời gian vật đi từ t=0 (\[x = \frac{A}{2}\]) đến t = 2,5s (x = 0) là:
\[\Delta t = 2,5s = \frac{T}{6} + \frac{T}{4} = \frac{{5T}}{{12}}\]
\[ \to T = 6s \to \omega = \frac{{2\pi }}{T} = \frac{\pi }{3}rad/s\]
Tại t = 0: \[\left\{ {\begin{array}{*{20}{c}}{x = A\cos \varphi = 2}\\{v = - A\omega \sin \varphi >0}\end{array}} \right. \to \left\{ {\begin{array}{*{20}{c}}{\cos \varphi = \frac{2}{4} = \frac{1}{2}}\\{\sin \varphi < 0}\end{array}} \right.\]
\[ \Rightarrow \varphi = - \frac{\pi }{3}\]
\[ \Rightarrow x = 4\cos \left( {\frac{\pi }{3}t - \frac{\pi }{3}} \right)cm\]
Đáp án cần chọn là: A
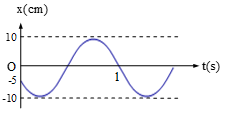
Câu 6
A. \[x = 10\cos \left( {\frac{{11\pi }}{6}t + \frac{{2\pi }}{3}} \right)cm\]
B. \[x = 10\cos \left( {\frac{{11\pi }}{6}t - \frac{{2\pi }}{3}} \right)cm\]
C. \[x = 10\cos \left( {2\pi t + \frac{\pi }{3}} \right)cm\]
D. \[x = 10\cos \left( {\frac{{5\pi }}{6}t - \frac{\pi }{3}} \right)cm\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
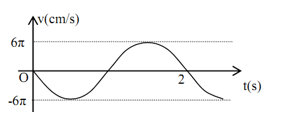
Câu 7
A. \[x = 6\cos \left( {\pi t + \frac{\pi }{2}} \right)cm\]
B. \[x = 6\cos \left( {\pi t} \right)cm\]
C. \[x = 6\cos \left( {\pi t - \frac{\pi }{2}} \right)cm\]
D. \[x = 6\sin \left( {\pi t} \right)cm\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \[x = 4\cos \left( {10\sqrt 5 t + \frac{\pi }{3}} \right)cm\]
B. \[x = 2\sqrt 2 \cos \left( {10\sqrt 5 t + \frac{\pi }{3}} \right)cm\]
C. \[x = 4\cos \left( {10\sqrt 5 t - \frac{\pi }{3}} \right)cm\]
D. \[x = 5\sin \left( {10\sqrt 5 t + \frac{\pi }{2}} \right)cm\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \[x = 8\cos \left( {\pi t - \frac{\pi }{3}} \right)cm\]
B. \[x = 8\cos \left( {\pi t - \frac{{2\pi }}{3}} \right)cm\]
C. \[x = 8\cos \left( {\pi t + \frac{\pi }{3}} \right)cm\]
D. \[x = 8\cos \left( {\pi t + \frac{{2\pi }}{3}} \right)cm\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \[x = 8\cos \left( {2\pi t - \frac{\pi }{2}} \right)cm\]
B. \[x = 4\cos \left( {\pi t + \frac{\pi }{2}} \right)cm\]
C. \[x = 8\cos \left( {2\pi t + \frac{\pi }{2}} \right)cm\]
D. \[x = 4\cos \left( {\pi t - \frac{\pi }{2}} \right)cm\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \[a = - 2\pi \cos \left( {2\pi t + \frac{\pi }{6}} \right)cm/{s^2}\]
B. \[a = 40\sin \left( {2\pi t + \frac{\pi }{6}} \right)cm/{s^2}\]
C. \[a = - 40\cos \left( {2\pi t + \frac{\pi }{6}} \right)cm/{s^2}\]
D. \[a = 2\pi \cos \left( {2\pi t + \frac{\pi }{6}} \right)cm/{s^2}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \[\frac{\pi }{2} < \varphi < \pi \]
B. \[\frac{\pi }{2} < \varphi < 0\]
C. \[ - \pi < \varphi < - \frac{\pi }{2}\]
D. \[0 < \varphi < \frac{\pi }{2}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
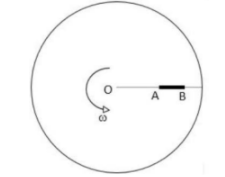
Câu 13
A. Thanh quay đi một góc rồi dừng lại.
B. Thanh quay tròn.
C.Thanh dao động quanh vị trí cân bằng.
D. Chuyển động của thanh có dạng phức tạp hơn các trường hợp trên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.