Câu hỏi:
12/11/2024 394
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Gọi \(M,N,P\) lần lượt là trung điểm các cạnh \(AB,BC,C'D'\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
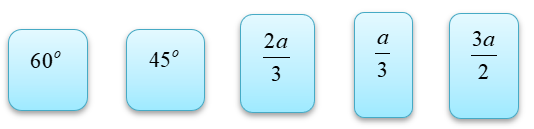
Độ dài đoạn thẳng \(AP\) là _______
Góc giữa hai đường thẳng \(MN\) và \(AP\) là _______
Khoảng cách giữa hai đường thẳng \(MN\) và \(AP\) là _______
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Gọi \(M,N,P\) lần lượt là trung điểm các cạnh \(AB,BC,C'D'\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Độ dài đoạn thẳng \(AP\) là _______
Góc giữa hai đường thẳng \(MN\) và \(AP\) là _______
Khoảng cách giữa hai đường thẳng \(MN\) và \(AP\) là _______
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
Độ dài đoạn thẳng \(AP\) là \(\frac{{3a}}{2}\)
Góc giữa hai đường thẳng \(MN\) và \(AP\) là \({45^o}\)
Khoảng cách giữa hai đường thẳng \(MN\) và \(AP\) là \(\frac{a}{3}\)
Phương pháp giải
- Sử dụng định lí Pytago.
- Áp dụng định lý cosin cho \(\Delta ACP\).
- Chuyển đổi đỉnh và sử dụng công thức tính thể tích để tính khoảng cách.
Lời giải
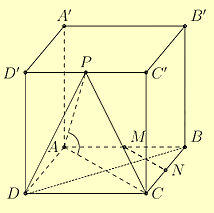
Do \(AC\) song song với \(MN\) nên góc giữa hai đường thẳng \(MN\) và \(AP\) bằng góc giữa hai đường thẳng \(AC\) và \(AP\).
\(PC = \sqrt {C'{C^2} + C'{P^2}} = \frac{{a\sqrt 5 }}{2}\)
\(AP = \sqrt {A'{A^2} + A'{P^2}} = \sqrt {{{\left( {\frac{{a\sqrt 5 }}{2}} \right)}^2} + {a^2}} = \frac{{3a}}{2}\)
Ta có: \(AC = a\sqrt 2 \).
Áp dụng định lý cosin cho ta có
\({\rm{cos}}\widehat {CAP} = \frac{{A{P^2} + A{C^2} - P{C^2}}}{{2AP.AC}} = \frac{{\frac{{9{a^2}}}{4} + 2{a^2} - \frac{{5{a^2}}}{4}}}{{2.\frac{{3a}}{2}.a\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\)
\( \Rightarrow \widehat {CAP} = {45^ \circ }\).
Vây góc giữa hai đường thẳng \({\rm{MN}}\) và \({\rm{AP}}\) bằng \({45^ \circ }\).
Khoảng cách giữa hai đường thẳng \({\rm{MN}}\) và \({\rm{AP}}\) bằng khoảng cách giữa \({\rm{MN}}\) và mặt phẳng \(\left( {APC} \right)\).
\(d\left( {MN,\left( {APC} \right)} \right) = d\left( {M,\left( {APC} \right)} \right)\)
\( = \frac{1}{2}d\left( {B,\left( {APC} \right)} \right) = \frac{1}{2}d\left( {D,\left( {APC} \right)} \right)\)
\( = \frac{1}{2}.\frac{{3{V_{D.APC}}}}{{{S_{APC}}}}\)
Ta có: \({S_{APC}} = \frac{1}{2}.AP.AC.{\rm{sin}}{45^ \circ } = \frac{1}{2}.\frac{{3a}}{2}.a\sqrt 2 .\frac{{\sqrt 2 }}{2} = \frac{{3{a^2}}}{4}\)
\({V_{D.APC}} = \frac{1}{3}.A'A.{S_{ACD}} = \frac{1}{3}.a.\frac{{{a^2}}}{2} = \frac{{{a^3}}}{6}\)
\( \Rightarrow d\left( {MN,AP} \right) = \frac{1}{2}.\frac{{3.\frac{{{a^3}}}{6}}}{{\frac{{3{a^2}}}{4}}} = \frac{a}{3}\)
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp giải
Dựa vào nhiệt độ sôi của nước và etanol, chất nào bay hơi trước thì sẽ giảm nồng độ trước.
Lời giải
Khi chưng cất rượu nấu, etanol có nhiệt độ sôi thấp hơn nước sẽ bay hơi trước nên tỉ lệ etanol/nước sẽ tăng dần. Vậy nhận định trên là nhận định sai.
Chọn B
Lời giải
Phương pháp giải
Lời giải
Để \(\widehat {\vec u,\vec v)} < {90^ \circ } \Rightarrow {\rm{cos}}\widehat {\left( {\vec u,\vec v} \right)} > 0\).
\( \Rightarrow \vec u.\vec v > 0 \Leftrightarrow 3 + {\rm{lo}}{{\rm{g}}_3}5.{\rm{lo}}{{\rm{g}}_5}3 + 4{\rm{lo}}{{\rm{g}}_m}2 > 0\)
\( \Leftrightarrow 4 + 4{\rm{lo}}{{\rm{g}}_m}2 > 0 \Leftrightarrow {\rm{lo}}{{\rm{g}}_m}2 > - 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > 1}\\{m < \frac{1}{2}}\end{array}} \right.\).
Kết hợp điều kiện \(m > 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{m > 1}\\{0 < m < \frac{1}{2}}\end{array}} \right.\)
Chọn D
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận