III. Vận dụng
Một bồn chứa xăng hình trụ có đường kính đáy \[2,2{\rm{\;m}}\] và chiều cao \[3,5{\rm{\;m}}.\] Biết rằng, cứ \[1\,\,kg\] sơn thì sơn được \[8{\rm{\;}}{{\rm{m}}^2}.\] Giả sử bề dày thành bồn chứa xăng không đáng kể và lấy \[\pi \approx 3,14.\] Hỏi để sơn bề mặt ngoài của bồn chứa xăng hết bao nhiêu ki-lô-gam sơn (kết quả làm tròn đến hàng đơn vị)?
A. \[1\] kg sơn.
B. \[2\] kg sơn.
C. \[3\] kg sơn.
D. \[4\] kg sơn.
Câu hỏi trong đề: Trắc nghiệm Bài tập cuối chương 10 lớp 9 (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
Bán kính đáy của bồn chứa xăng là: \[r = \frac{{2,2}}{2} = 1,1{\rm{\;(m)}}{\rm{.}}\]
Diện tích toàn phần của bồn chứa xăng là:
\[{S_{tp}} = 2\pi r\left( {h + r} \right) = 2\pi \cdot 1,1 \cdot \left( {3,5 + 1,1} \right) = 10,12\pi {\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Số ki-lô-gam sơn cần dùng để sơn bề mặt ngoài của bồn chứa xăng là:
\[\frac{{10,12\pi }}{8} \approx \frac{{10,12 \cdot 3,14}}{8} \approx 4\,\,\left( {kg} \right)\].
Vậy ta chọn phương án D.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[0,343{\rm{\;}}{{\rm{m}}^3}.\]
B. \[0,343\pi {\rm{\;}}{{\rm{m}}^3}.\]
C. \[0,49\pi {\rm{\;}}{{\rm{m}}^3}.\]
D. \[0,147\pi {\rm{\;}}{{\rm{m}}^3}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
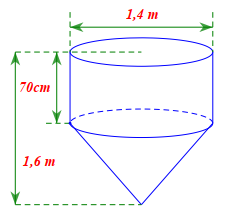
Gọi \[{V_1},{r_1},{h_1}\] lần lượt là thể tích, bán kính đáy, chiều cao của phần hình trụ.
\[{V_2},{r_2},{h_2}\] lần lượt là thể tích, bán kính đáy, chiều cao của phần hình nón.
Suy ra \[{r_2} = {r_1}.\]
Đổi: \[70{\rm{\;cm}} = 0,7{\rm{\;m}}.\]
Bán kính đáy của phần hình trụ, hình nón là: \[{r_1} = {r_2} = \frac{{1,4}}{2} = 0,7{\rm{\;(m)}}{\rm{.}}\]
Thể tích của phần hình trụ là:
\[{V_1} = \pi r_1^2{h_1} = \pi \cdot 0,{7^2} \cdot 0,7 = 0,343\pi {\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Chiều cao của phần hình nón là: \[{h_2} = 1,6 - 0,7 = 0,9{\rm{\;(m)}}{\rm{.}}\]
Thể tích của phần hình nón là:
\[{V_2} = \frac{1}{3}\pi r_2^2{h_2} = \frac{1}{3}\pi \cdot 0,{7^2} \cdot 0,9 = 0,147\pi {\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Thể tích của dụng cụ đã cho là:
\[V = {V_1} + {V_2} = 0,343\pi + 0,147\pi = 0,49\pi {\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Vậy ta chọn phương án C.
Câu 2
A. \[80\pi {\rm{\;c}}{{\rm{m}}^2}.\]
B. \[20\pi {\rm{\;c}}{{\rm{m}}^2}.\]
C. \[90\pi {\rm{\;c}}{{\rm{m}}^2}.\]
D. \[40\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
Bán kính đáy của hình trụ đó là: \[r = \frac{{10}}{2} = 5{\rm{\;(cm)}}{\rm{.}}\]
Diện tích xung quanh của hình trụ đó là: \[{S_{xq}} = 2\pi rh = 2\pi \cdot 5 \cdot 4 = 40\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Vậy ta chọn phương án D.
Câu 3
A. \[3\sqrt 2 {\rm{\;cm}}.\]
B. \[6\sqrt 2 {\rm{\;cm}}.\]
C. \[6{\rm{\;cm}}.\]
D. \[12{\rm{\;cm}}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. hình chữ nhật.
B. đường tròn.
C. đường tròn lớn.
D. hình tròn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[4\pi \sqrt 3 {\rm{\;c}}{{\rm{m}}^2}.\]
B. \[\pi \sqrt {39} {\rm{\;c}}{{\rm{m}}^2}.\]
C. \[8\pi \sqrt 3 {\rm{\;c}}{{\rm{m}}^2}.\]
D. \[12\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[12{\rm{\;dm}}.\]
B. \[9{\rm{\;dm}}.\]
C. \[6{\rm{\;dm}}.\]
D. \[3{\rm{\;dm}}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập