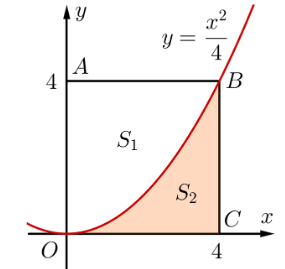
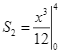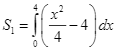Cho parabol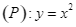 
và hai điểm 
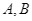thuộc 
sao cho 
. Biết 
sao cho diện tích hình phẳng giới hạn bởi và đường thẳng 
đạt giá trị lớn nhất. Tìm 
.
và hai điểm thuộc 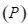sao cho 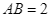. Biết 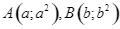sao cho diện tích hình phẳng giới hạn bởi 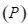và đường thẳng 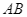đạt giá trị lớn nhất. Tìm 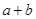.Quảng cáo
Trả lời:
Giải bởi Vietjack
Trả lời: 0
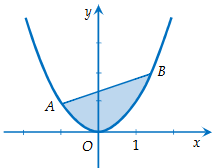
Giả sử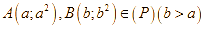 
sao cho 
.
Phương trình đường thẳng 
.
Gọi
là diện tích hình phẳng cần tìm, ta có
.
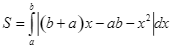
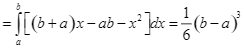Vì nên 
.
Dấu bằng xảy ra khi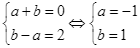 
. Suy ra 
.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: 2250
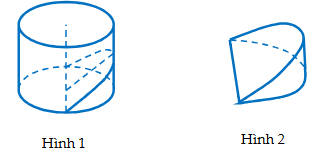
Chọn hệ trục tọa độ như hình vẽ.
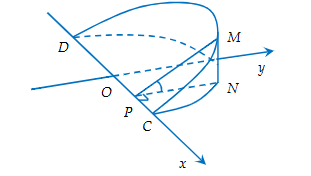
Khi đó hình nêm có đáy là nửa hình tròn có phương trình 
.
Một mặt phẳng cắt vuông góc với trục 
tại điểm có hoành độ 
cắt hình nêm theo thiết diện có diện tích là 
.
Ta có 
và 
.
Khi đó 
.
Suy ra thể tích hình nêm là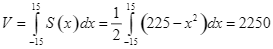 
cm3.
Câu 2
A. 
.
.B. 
.
. C. 
.
.D. 
.
.Lời giải
Đáp án đúng là: C
nhận 
làm vectơ pháp tuyến
Mặt phẳng đã cho song song với nên cũng nhận nhận làm vectơ pháp tuyến
Vậy mặt phẳng đi qua 
và song song với có phương trình là
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập