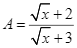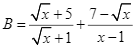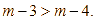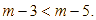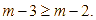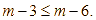Câu hỏi:
11/12/2024 126
Trên nóc của một tòa nhà có một cột ăng – ten cao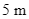 
. Từ vị trí quan sát 
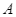cao 
so với mặt đất, có thể nhìn thấy đỉnh 
và đỉnh 
của một cột ăng – ten dưới góc 
và 
so với phương nằm ngang. Tính chiều cao của tòa nhà.
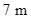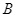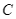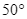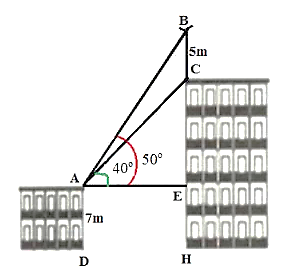
. Từ vị trí quan sát cao so với mặt đất, có thể nhìn thấy đỉnh và đỉnh của một cột ăng – ten dưới góc và 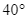so với phương nằm ngang. Tính chiều cao của tòa nhà.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chiều cao của tòa nhà chính là độ dài đoạn thẳng 
.
Xét tam giác 
vuông tại 
, ta có:
(1).
Xét tam giác 
vuông ở 
, ta có:
(2).
Từ (1) và (2) suy ra 
.
Suy ra 
Chiều cao của tòa nhà là: 
.
Vậy tòa nhà cao 
.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi 
(tấn) lần lượt là khối lượng quặng chứa 
sắt và 
sắt (
).
Theo đề, tổng khối lượng quặng là 
tấn nên ta có: 
. (1)
Khối lượng sắt trong tấn quặng chứa 
sắt là: 
(tấn).
Khối lượng sắt trong 
(tấn) quặng chứa sắt là: 
(tấn).
Khối lượng sắt trong 
(tấn) quặng chứa sắt là: 
(tấn).
Do đó, ta có phương trình: 
. (2)
Từ (1) và (2) ta có hệ phương trình: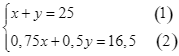 
.
Từ phương trình (1), suy ra 
.
Thay vào phương trình (2) ta được:
(thỏa mãn).
Thay vào phương trình , ta được 
(thỏa mãn).
Vậy cần trộn 16 tấn quặng chứa sắt và 9 tấn quặng chứa sắt để được tấn quặng chứa sắt.
Câu 2
Giải bài toán sau bằng cách lập bất phương trình:
Người ta dùng một loại xe tải để chở bia cho một nhà máy. Mỗi thùng bia 24 lon nặng trung bình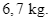 
Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là 
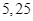tấn. Hỏi xe có thể chở được tối đa bao nhiêu thùng bia, biết bác tài xế nặng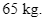 
Giải bài toán sau bằng cách lập bất phương trình:
Người ta dùng một loại xe tải để chở bia cho một nhà máy. Mỗi thùng bia 24 lon nặng trung bình Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là tấn. Hỏi xe có thể chở được tối đa bao nhiêu thùng bia, biết bác tài xế nặng
Lời giải
Đổi 
tấn = 
kg.
Gọi 
là số thùng bia mà xe có thể chở (
, đơn vị: thùng).
Khối lượng của thùng bia là: 
(kg).
Tổng khối lượng của các thùng bia và bác tài xế là: 
(kg).
Theo bài, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là tấn nên ta có bất phương trình: 
.
Giải bất phương trình:
.
Mà và cần tìm có giá trị lớn nhất nên 
Vậy xe có thể chở được tối đa 
thùng bia.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận