Trong không gian Oxyz, cho hai điểm \(A\left( {1;2;1} \right);B\left( {2; - 1;3} \right)\) và điểm \(M\left( {a;b;0} \right)\) sao cho \(M{A^2} + M{B^2}\) nhỏ nhất. Tính \(a + b\).
Trong không gian Oxyz, cho hai điểm \(A\left( {1;2;1} \right);B\left( {2; - 1;3} \right)\) và điểm \(M\left( {a;b;0} \right)\) sao cho \(M{A^2} + M{B^2}\) nhỏ nhất. Tính \(a + b\).
Quảng cáo
Trả lời:
Ta thấy \(M\left( {a;b;0} \right) \in \left( {Oxy} \right)\). Gọi \(I\left( {\frac{3}{2};\frac{1}{2};2} \right)\) là trung điểm của đoạn thẳng \(AB\).
Ta có \(M{A^2} + M{B^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} = {\left( {\overrightarrow {IA} - \overrightarrow {IM} } \right)^2} + {\left( {\overrightarrow {IB} - \overrightarrow {IM} } \right)^2}\)
\( = 2I{M^2} + 2I{A^2} = 2I{M^2} + 7\).
Suy ra \(M{A^2} + M{B^2}\) nhỏ nhất Û \(IM\) ngắn nhất Û \(M\) là hình chiếu vuông góc của \(I\) trên mặt phẳng \(\left( {Oxy} \right)\).
Suy ra \(M\left( {\frac{3}{2};\frac{1}{2};0} \right)\). Như vậy \(a = \frac{3}{2};b = \frac{1}{2} \Rightarrow a + b = \frac{3}{2} + \frac{1}{2} = 2\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) S, b) S, c) S, d) Đ
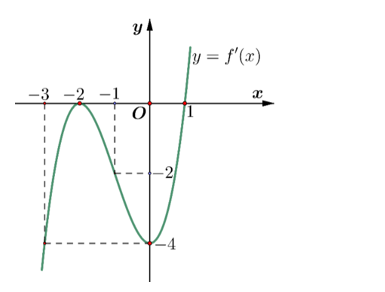
a) Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right) \ge 0\) với \(\forall x \ge 1\) nên hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
b) Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right)\) chỉ đổi dấu một lần qua \(x = 1\) nên hàm số có một điểm cực trị.
c) Từ đồ thị ta có hàm số \(f'\left( x \right)\) có dạng: \(f'\left( x \right) = a{\left( {x + 2} \right)^2}\left( {x - 1} \right)\).
Đồ thị hàm số \(y = f'\left( x \right)\) đi qua \(\left( {0; - 4} \right)\) nên: \( - 4 = a{\left( {0 + 2} \right)^2}\left( {0 - 1} \right) \Leftrightarrow a = 1\).
Vậy \(f'\left( x \right) = {\left( {x + 2} \right)^2}\left( {x - 1} \right) \Rightarrow f'\left( 2 \right) = {\left( {2 + 2} \right)^2}\left( {2 - 1} \right) = 16\).
d) Ta có: \(g'\left( x \right) = f'\left( x \right) - x + 1 = 0 \Leftrightarrow f'\left( x \right) = x - 1\).
Vẽ đường thẳng \(y = x - 1\) trên cùng hệ trục tọa độ với đồ thị hàm số \(y = f'\left( x \right)\).
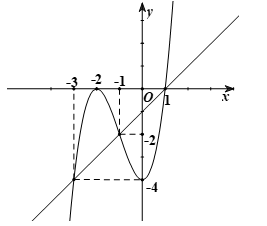
Khi đó: \(f'\left( x \right) = x - 1 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 1\\x = 1\end{array} \right.\).
Bảng biến thiên của hàm số \(g\left( x \right)\).
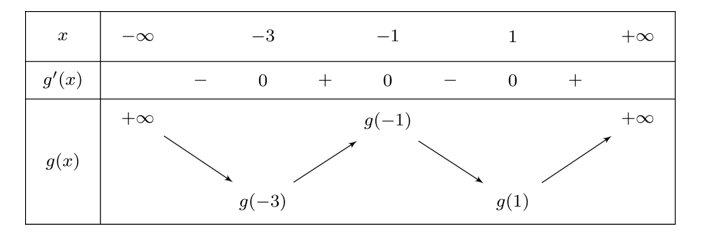
Ta có hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - 3; - 1} \right)\) nên \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - \frac{5}{2}; - \frac{3}{2}} \right)\).
Lời giải
Lợi nhuận doanh nghiệp thu được là \(h\left( x \right) = \left( {2000x - {x^2}} \right) - \left( {{x^2} + 1440x + 50} \right) - tx\)
\( = - 2{x^2} + \left( {560 - t} \right)x - 50\) với \(0 < x \le 2000\).
Xét hàm \(h\left( x \right) = - 2{x^2} + \left( {560 - t} \right)x - 50\) với \(0 < x \le 2000\).
Ta có \(h'\left( x \right) = - 4x + 560 - t = 0 \Rightarrow x = \frac{{560 - t}}{4} \in \left( {0;2000} \right)\).
Bảng biến thiên
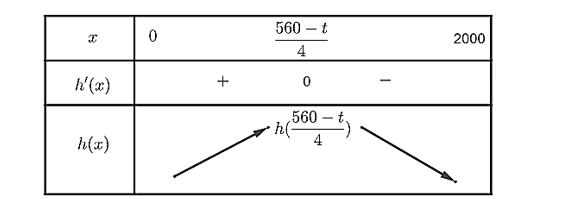
Từ bảng biến thiên ta thấy lợi nhuận doanh nghiệp cao nhất tại \(x = \frac{{560 - t}}{4}\).
Khi đó số tiền thuế thu được từ doanh nghiệp là \(k\left( t \right) = \frac{{560 - t}}{4}.t = - \frac{{{t^2}}}{4} + \frac{{560}}{4}t\) với \(0 < t < 300\).
Bảng biến thiên
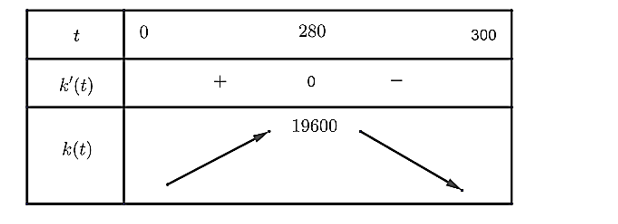
Từ bảng biến thiên ta thấy mức thuế phụ thu trên một đơn vị sản phẩm bán được là \(t = 280 \Rightarrow x = 70\) sản phẩm.
Vậy mức thuế phụ thu là 2800000 đồng/ sản phẩm, doanh nghiệp sản xuất và bán hết 70 sản phẩm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
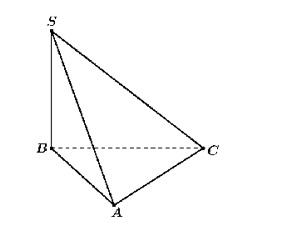
A. \(60^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
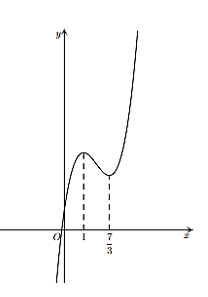
A. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( {\frac{7}{3}; + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.