Cho tam giác ABC vuông tại A. Tính tỉ số lượng giác của góc B trong mỗi trường hợp sau:
a) BC = 5 cm; AB = 3 cm.
b) AB = 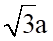 ; AC = a.
; AC = a.
Cho tam giác ABC vuông tại A. Tính tỉ số lượng giác của góc B trong mỗi trường hợp sau:
a) BC = 5 cm; AB = 3 cm.
b) AB = ; AC = a.
Quảng cáo
Trả lời:
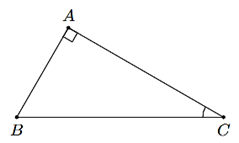
a) Áp dụng định lí Pythagore vào tam giác ABC, ta được: AC = \(\sqrt {{5^2} - {3^2}} = 4\) cm.
Ta có: sin B = \(\frac{{AC}}{{BC}} = \frac{4}{5}\); cos B = \(\frac{{AB}}{{BC}} = \frac{3}{5}\); tan B = \(\frac{{AC}}{{AB}} = \frac{4}{3}\); cot B = \(\frac{{AB}}{{AC}} = \frac{3}{4}\).
b) Áp dụng định lí Pythagore vào tam giác ABC, ta được: BC = \(\sqrt {3{a^2} + {a^2}} = 2a\).
Ta có: sin B = \(\frac{{AC}}{{BC}} = \frac{a}{{2a}} = \frac{1}{2}\); cos B = \(\frac{{AB}}{{BC}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}\);
tan B = \(\frac{{AC}}{{AB}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }}\); cot B = \(\frac{{AB}}{{AC}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Tam giác ABC vuông tại B.
B. sin A = \(\frac{{\sqrt {15} }}{5}\).
C. cos A = \(\frac{{\sqrt {10} }}{5}\).
D. tan A = \(\frac{{\sqrt 6 }}{2}\).
Lời giải
Đáp án đúng là: A
Áp dụng định lí Pythagore đảo, ta có:
AC2 + BC2 = 3a2 + 2a2 = 5a2 = AB2.
Do đó, tam giác ABC vuông tại C.
Ta có: sin A = \(\frac{{BC}}{{AB}} = \frac{{\sqrt 3 }}{{\sqrt 5 }} = \frac{{\sqrt {15} }}{5}\);
cos A = \(\frac{{AC}}{{AB}} = \frac{{\sqrt 2 }}{{\sqrt 5 }} = \frac{{\sqrt {10} }}{5}\);
tan A = \(\frac{{BC}}{{AC}} = \frac{{\sqrt 3 }}{{\sqrt 2 }} = \frac{{\sqrt 6 }}{2}\).
Câu 2
A. sin B = cos C = \(\frac{4}{5}\).
B. tan B = tan C = \(\frac{3}{4}\).
C. sin C = cot B = \(\frac{4}{5}\).
D. tan C = cot B = \(\frac{4}{3}\).
Lời giải
Đáp án đúng là: D
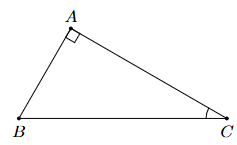
Áp
dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:AB2 + AC2 = BC2
1,62 + 1,22 = BC2
Suy ra BC = 2 cm.
Ta có: sin B = cos C = \(\frac{{AC}}{{BC}} = \frac{{1,2}}{2} = \frac{3}{5}\);
tan B = cot C = \(\frac{{AC}}{{AB}} = \frac{{1,2}}{{1,6}} = \frac{3}{4}\);
sin C = cos B = \(\frac{{AB}}{{BC}} = \frac{{1,6}}{2} = \frac{4}{5}\);
tan C = cot B = \(\frac{{AB}}{{AC}} = \frac{{1,6}}{{1,2}} = \frac{4}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{2}{3}\).
B. \(\frac{3}{2}\).
C. \(\frac{2}{{\sqrt {13} }}\)
D.\(\frac{3}{{\sqrt {13} }}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Tam giác MNP vuông tại M.
B. sin N = \(\frac{{12}}{{13}}\).
C. cos N = \(\frac{5}{{13}}\).
D. tan N = \(\frac{5}{{12}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. tan B = \(\frac{3}{4}\).
B. cot B = \(\frac{4}{3}\).
C. sin C = 0,6.
D. cos C = 0,4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.