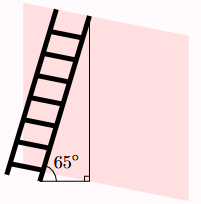
Một cây cau có chiều cao 6 m. Để hái một buồng cau xuống, phải đặt thang tre sao cho đầu thang tre đạt độ cao đó, khi đó góc của thang tre với mặt đất là bao nhiêu, biết thang dài 8 m (làm tròn đến chữ số phần chục của phút).
A. 48°35’.
B. 48°36’.
C. 48°4’.
D. 48°5’.
Quảng cáo
Trả lời:
Đáp án đúng là: A
Bài toán được mô tả bằng hình học như sau:
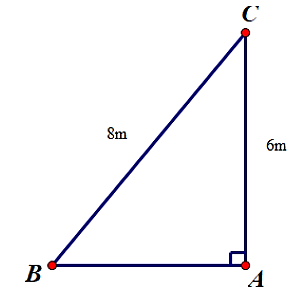
Xét tam giác ABC vuông tại A, ta có:
sin B = \(\frac{{AC}}{{BC}} = \frac{6}{8} = \frac{3}{4}\) (tỉ số lượng giác của góc nhọn)
Suy ra \(\widehat B\) ≈ 48°35’.
Vậy góc giữa thang tre với mặt đất là 48°35’.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
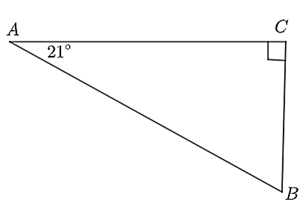
a) Xét tam giác ABC vuông tại C, ta có:
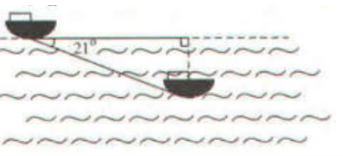
sin A = \(\frac{{BC}}{{AB}}\), suy ra BC = AB.sin A = 250.sin 21° ≈ 89,6 m.
Vậy tàu đi được 250 m thì tàu ở độ sau khoảng 89,6 m.
b) Đổi 9 km/h = 2,5 m/s.
Gọi t (giây) là thời gian đi để tàu đạt được độ sâu 200 m.
Quãng đường tàu đi được trong thời gian t (giây) là:
AB = SAB = v.t = 2,5t (m)
Xét tam giác ABC vuông tại C, ta có:
sin A = \(\frac{{BC}}{{AB}}\) hay sin 21° = \(\frac{{200}}{{2,5t}}\) suy ra t = \(\frac{{200}}{{2,5\sin 21^\circ }}\)≈ 223 s ≈ 4 phút.
Vậy thời gian của tàu là khoảng 4 phút.
Câu 2
A. 6 m.
B. 5,9 m.
C. 5,8 m.
D. 5 m.
Lời giải
Đáp án đúng là: A
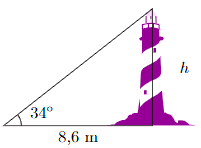
Ta nhận thấy đường cao tháp đối diện với góc 34° (góc tạo với tia nắng mặt trời và bóng của tháp trên mặt đất).
Do đó, ta có: h = 8,6.tan34° ≈ 6 (m).
Vậy chiều cao của tháp là khoảng 6 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 1,3 m.
B. 1 m.
C. 1,38 m.
D. 1,4 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.